汽车液力变矩器特性曲线详解

液力变矩器特性的变化规律是以曲线表示的，这种曲线称为液力变矩器的特性曲线。

1.液力变矩器的输出特性曲线

输出特性曲线是在测功实验台试验并经计算得出的，如图14-7所示。

2.液力变矩器的原始特性曲线

液力变矩器的原始特性曲线，是指液力变矩器的泵轮力矩系数λ_B和变矩系数K、效率η与传动比i的关系曲线。几何相似的液力变矩器，其原始特性曲线都一样，所以原始特性曲线又称类型特性曲线。原始特性曲线是由输出特性曲线计算得出的。原始特性曲线即为K=f（i）、η=f（i）和λ_B=f（i）的关系图线，如图14-8所示。

图14-7 液力变矩器的输出特性曲线

图14-8 液力变矩器的原始特性曲线

变矩系数和效率公式分别为

在以上两式中，当λ_B和λ_T已知时，可以根据一定的传动比i计算确定K和η值，反之，当知道λ_B和K值时，也可以计算其他值。

3.液力变矩器的输入特性曲线(www.xing528.com)

表示泵轮转矩M_B与转速n_B之间关系的曲线称为液力变矩器的输入特性曲线（图14-9）。对于给定的变矩器，用给定的工作液体在给定的工况下运转时，λ_BγD⁵=常数。

这样得出的输入特性曲线为一条通过坐标原点的抛物线，一般又称为负载抛物线，而在变工况下，因λ_B与传动比有关，输入特性曲线为一组抛物线束，抛物线束的宽度由λ_B的变化幅度决定，而λ_B的变化幅度是由透穿性所决定的。除输入特性i=0的一组由试验测得外，其余均由计算得到。输入特性供变矩器与发动机匹配选型时参考。

4.液力变矩器的通用特性曲线

在n_B=常数条件下的一组M_T=f（n_T），和η=常数条件下的一组M_T=f（n_T）的关系图线称为通用特性曲线（图14-10），它是根据原始特性曲线计算得出的。图中n_B、n′_B、n″_B、n‴_B、n″″_B曲线分别表示泵轮转速为n_B、n′_B、n″_B、n‴_B、n″″_B时，M_T与n_T的关系（n_B、>n′_B>n″_B＞n‴_B＞n″″_B）。

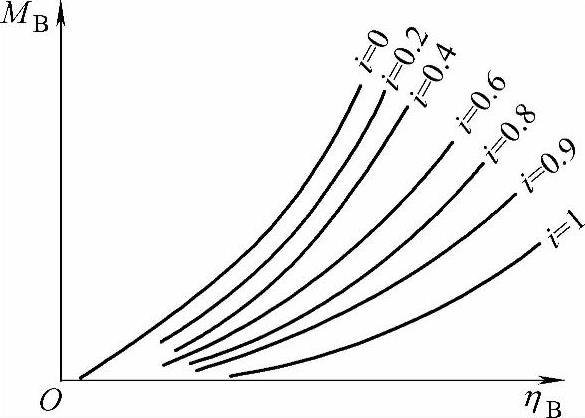
图14-9 液力变矩器的输入特性曲线

图14-10 液力变矩器的通用特性曲线

等效率的M_T=f（n_T），曲线为通过坐标原点的抛物线，因为

在曲线图上，平滑地连接效率值相同的各点，在相应的曲线上标以效率数值η₁、η₂、η3、η4、η5，其中η1>η2>η3>η4。通用特性曲线的任一点，决定了液力变矩器的工况，即决定了M_T、n_B、n_T及η值。如图中C点，表示在此工况下，液力变矩器涡轮力矩M_T=M_C，涡轮转速n_T=n_C，泵轮转速n_B=n‴_B，液力变矩器效率η=η₂。求得这些值后还可计算得到变矩系数K及泵轮力矩M_B，因为，，式中i、η、M_T及K是已知的。