汽车液力变矩器基本特性

1.液力变矩器工作轮的力矩方程式

在匀速运动的情况下，液力变矩器的所有工作轮的力矩代数和为零，即

∑M_i=M_B+M_D+（-M_T） （14-16）

式中 M_B——发动机作用于泵轮轴的力矩，即泵轮叶片对液流作用的力矩；

-M_T——工作机构作用于涡轮轴的力矩，即涡轮叶片对液流的力矩，而涡轮输出力矩

则为M_T；

M_D——壳体作用于导轮的反转矩。

因此

M_T=M_B+M_D （14-17）

一般情况下M_D>0，所以M_T>M_B，即涡轮转矩大于泵轮转矩。

2.液力变矩器的变矩系数和传动比

1）变矩系数 液力变矩器的变矩能力用变矩系数K来表示，变矩系数是指液力变矩器涡轮转矩与泵轮转矩的比值。即

液力变矩器的变矩系数K又称变矩比，它不是一个常数，而是随着泵轮和涡轮转速不同而变化。

2）传动比。液力变矩器的涡轮转速与泵轮的转速之比称为液力变矩器的传动比，即

式中 i——液力变矩器的传动比；

n_T——涡轮转速（r/min）；

n_B——泵轮转速（r/min），它一般等于发动机转速。

3.液力变矩器的效率

根据能量守恒定律，液力变矩器的泵轮与涡轮的转矩和转速存在如下关系

n_BM_Bη=n_TM_T(www.xing528.com)

因此，变矩器效率为

液力变矩器有一个最高效率工况，因为在设计液力变矩器时，是在一个计算工况下进行计算的，已给定了泵轮的转速及一个计算传动比i，在该工况下所计算出的各工作轮叶片入口及出口角度，是与叶片入口处相对速度方向一致的，这时，变矩器具有高效率，液流可以无冲击地进入工作轮的叶片通道。但在其他工况时，已定的叶片进口角度不能与液流方向一致而产生了冲击损失，角度差得越大，损失也越大，效率则显著降低。因此液力变矩器的效率随传动比不同（即工况不同）而变化，并呈抛物线形状（图14-4）。也就是说液力变矩器只是在一定范围内具有较高的效率。

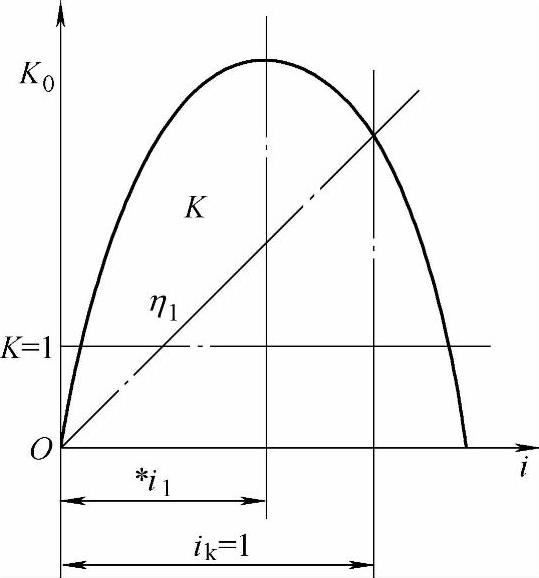
图14-4 液力变矩器效率与传动比关系曲线

液力变矩器效率最高时的工作情况称为最佳工况，此时各参数的左上角加符号“*”，如*n、*i等。

效率曲线形状完全取决于变矩系数曲线K的形状，曲线K不同时，效率曲线也不同。

曲线K越陡（K₀值较大），效率曲线越窄，最低效率也越低。如果K₀值较小，K的曲线越平坦。则效率曲线越宽，最高效率也越高。一般变矩器的最高效率可达85%～87%。

4.液力变矩器的计算方程

经过数学推导，可得到液力变矩器的计算方程为

M_B=λ_Bγn²_BD⁵ （14-21）

M_T=λ_Tγn²_BD⁵ （14-22）

式中 M_B——泵轮叶片作用于液流的力矩（N·m）；

M_T——液流作用于涡轮叶片的输出力矩（N·m）；

λ_B——泵轮力矩系数[min²/（m·r²）]，它是传动比i的函数，即λ_B=f（i）；

λ_T——涡轮力矩系数[min²/（m·r²）]，它也是传动比i的函数，即λ_T=f（i）；

γ——液体重度（N/m³）；

n_B——泵轮转速（r/min）；

D——变矩器的有效直径，即循环圆径向最大尺寸（m）。

力矩系数的物理意义：有效直径D=1m的液力变矩器，在转速n_B=1r/min及工作液体的重度γ=1N/m³的情况下工作时液力变矩器相应轴上的力矩值。