汽车液力变矩器的相似原理

相似原理在很多学科都得到了广泛应用。液力变矩器的相似原理实质上包括几何相似、运动相似和动力相似三个内容：

1）几何相似。如果两个液力变矩器其工作轮循环圆形状相同，对应的角度相等，对应尺寸成比例，则称这两个液力变矩器几何相似。

2）运动相似。如果两个液力变矩器，其流动状态相似，对应速度的方向相同，大小成比例，则称这两个液力变矩器运动相似。这种类似工况，称为等倾角工况，其外部特征为两个液力变矩器转速比i_TB=n_T/n_B相同。运动相似是建立在几何相似基础上的，没有几何相似，就不可能有运动相似。

3）动力相似。如果两个液力变矩器其流动状态相似，对应点上作用的同名力方向相同、大小成比例，则称这两个液力变矩器动力相似。

实际上，两种流动完全符合动力相似是不可能的。通常，只考虑影响流动规律的主要作用力，使这些主要作用力符合相似准则，而忽略次要的作用力。这种相似称为部分动力相似。液力传动中，主要作用力是惯性力和粘性力，所以，就用雷诺数Re来作为判断相似性的准则。雷诺数的物理意义是表示惯性力与粘性力之间的比值。如果两种流动的雷诺数相同，这就表示在两种情况下，惯性力及粘性力比值是相同的，即符合部分动力相似的条件。雷诺数值越大，则惯性力所占的比例越大；反之，则粘性力的比例就大。根据第2章中提到的雷诺数表达式，对于液流在工作轮中的流动，通常取循环圆过流部分的最大尺寸——有效直径为特征尺寸，以nD作为特性速度，所以雷诺数为

式中 n——转速；

D——工作轮有效直径；

ν——工作液体的运动粘度。

这一计算式对于液力耦合器或液力变矩器都适用。

根据相似理论，可以引出四个相似定律。称原有的液力变矩器为模型液力变矩器，以下标M表示，经放大或缩小后的液力变矩器称为实物液力变矩器，以下标H表示。图14-3所示为速度相似三角形。如果两个液力变矩器几何相似和运动相似，则它们各种速度、线性尺寸及转速之间有如下关系：

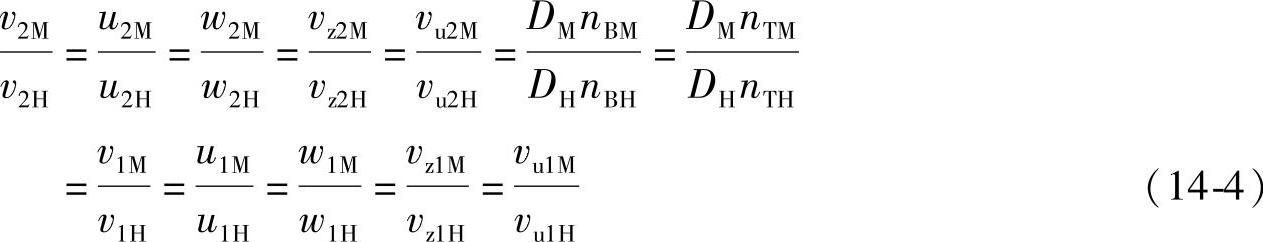
式中 D——液力变矩器任一线性尺寸，也可以认为是有效直径。

1.第一相似定律

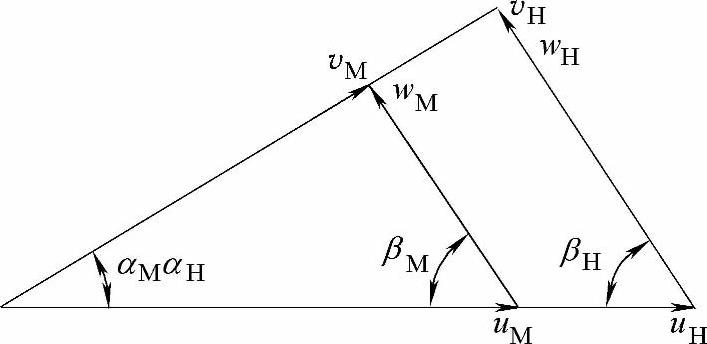
图14-3 速度相似三角形

用第一相似定律表示几何相似的液力变矩器，在相似工况下，其流量和转速与几何尺寸之间的关系。

由式（13-4）可知，液力变矩器的流量为

Q=Avz

式中 A——变矩器的通流截面积

则有

由式（14-4）知

将式（14-6）代入式（14-5）得

由于相对应的线性尺寸的比值为常数，可以用液力变矩器有效直径来代替别的线性尺寸。即用D²_M代替A_M，D²_H代替A_H，则式（14-7）可改写为

式（14-8）便是第一相似定律。它说明几何相似的液力变矩器在相似工况下，其流量比值与有效直径比值的三次方、泵轮转数的比值的一次方成正比。

2.第二相似定律(www.xing528.com)

用第二相似定律表示几何相似的液力变矩器，在相似工况下，其能头和几何尺寸与转速之间的关系。

由式（13-19）欧拉方程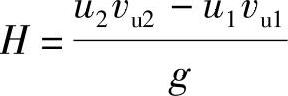可知两个液力变矩器的能头比为

同样由式（14-4）的比例关系可知

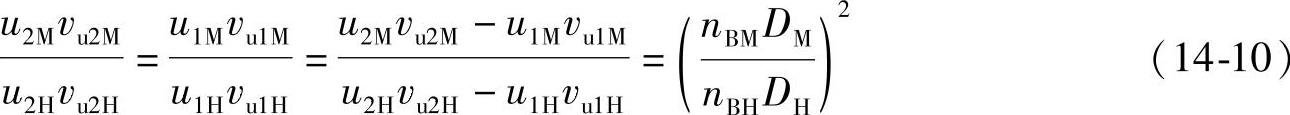
将式（14-10）代入式（14-9）得到第二相似定律的表达式

第二相似定律说明，几何相似的液力变矩器，在相似工况下，其能头比值与有效直径比值及泵轮转速比值的二次方成正比。

3.第三相似定律

用第三相似定律表示几何相似的液力变矩器，在相似工况下，其功率和几何尺寸与转速之间的关系。

液力变矩器的功率为 N=qγH

其功率比值为

将第一相似定律式（14-8）及第二相似定律式（14-11）代入式（14-12），则得

第三相似定律表达式

第三相似定律说明，几何相似的液力变矩器在相似工况下，其功率的比值与工作液体的重度比值一次方、泵轮转速比值的三次方和有效直径比值的五次方成正比。

4.第四相似定律

用第四相似定律进一步了解几何相似的液力变矩器，在相似工况下，其转矩和几何尺寸与转速之间的关系，作如下推导。

液力变矩器传递的功率为

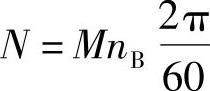
其功率比值为

将第一相似定律式（14-8）及第二相似定律式（14-11）代入式（14-14）则得

式（14-15）称为第四相似定律。此式说明，几何相似的液力变矩器在等倾角工况下，其转矩的比值与工作液体重度比值的一次方、泵轮转速比值的二次方和有效直径比值的五次方成正比。

在以上相似定律的表达式中，各符号的意义如下：Q——流量、H——能头、γ——工作液体的密度、D——液力变矩器的有效直径、n——工作轮的转速、N——液力变矩器所传递的功率、M——液力变矩器所传递的转矩。