汽车流体传动速度三角形+液体在工作轮的运动

液体在叶轮机械工作轮中的运动，是很复杂的空间运动。一方面，液体在工作轮中沿着叶片流道作相对运动，另一方面，又随工作轮作空间旋转运动——牵连运动。为了研究方便，在理论上做一些假设，从而使流动简化，总结出规律，然后再用实验的方法加以修正。这种简化的理论称为一元束流理论。具体假设如下：

1）运动的液体是理想液体。工作轮中的流动是稳定流动。因此液体流动是连续的、无粘性的、不可压缩的及在工作轮中液流是无摩擦损失的。

2）工作轮中叶片数无限多，且形状相同和厚度无限小，因而液流被分成无限多与叶片骨线一致的流束。

3）工作轮入口前的流动情况，取决于前一工作轮出口的流动情况。

4）工作轮出口的流动情况，不受工作轮入口流动情况的影响。

由上述假设，就可将液体沿工作轮复杂的空间运动，简化为理想液体的流束运动。这些理想液体在工作轮中的运动，可以分解为无穷多条完全相同的流束的运动。通过以上假设我们只需研究其中一条流束，就可以了解液体的全部运动。

流束速度在工作轮中的变化如图13-2所示。在研究中，采用下列符号规定速度三角形。

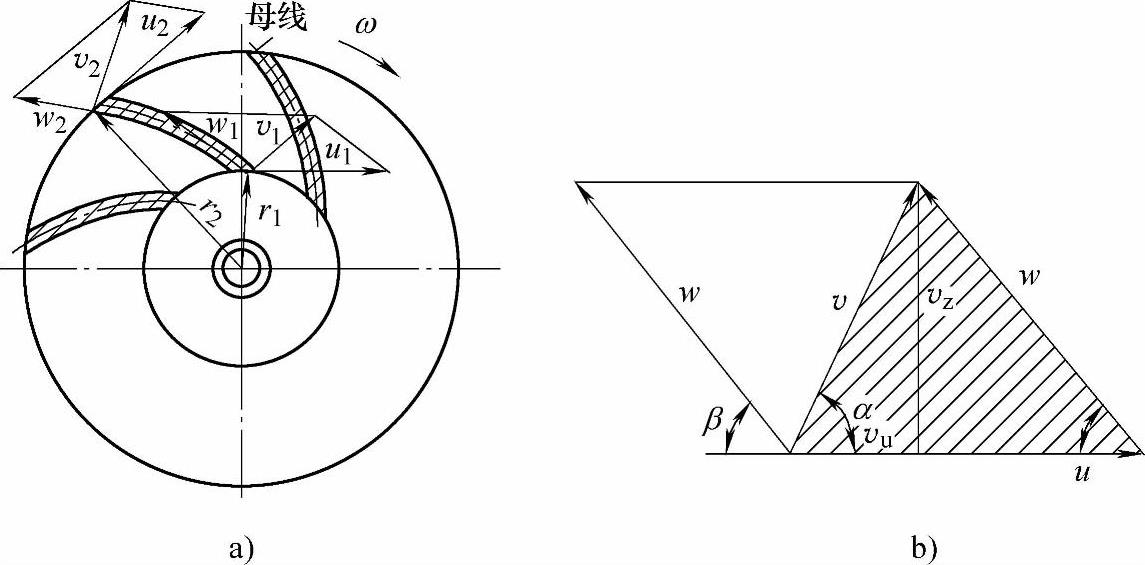
图13-2 流束速度在工作轮中的变化

a）液体质点在工作轮中的流动 b）速度三角形

ω——工作轮的角速度，取逆时针方向为正，反之为负（从主动轴方向看）（rad/s）；

u——工作轮的圆周速度（液体的牵连速度），其方向为圆周的切线方向（m/s）；

v——绝对速度（m/s）；

w——液体相对工作轮的相对速度，其方向为叶片的骨线方向（m/s）；

α——绝对速度v和圆周速度u之间的夹角；

β——圆周速度u和相对速度w之间的夹角；

下标1——表示工作轮入口；

下标2——表示工作轮出口。

根据速度矢量合成的定理有(www.xing528.com)

v=w+u （13-1）

液力传动中，由于工作轮叶片对液流的作用，使液体质点在工作轮进出口处的速度发生变化，通常采用由速度v、w、u组成的速度平行四边形来反映液流速度的矢量关系，又可以简化为一个封闭的速度三角形（图13-2b）。

在速度三角形中，将绝对速度v分解成两个相互垂直的分量v_u（m/s）与v_z（m/s）。其中，v_u为绝对速度v在圆周速度u方向上的投影；v_z为绝对速度v在半径方向上的投影，称为轴面分速度。即有

v_u=vcosα （13-2）

v_z=vsinα=（u-v_u）tanβ （13-3）

轴面分速度v_z的大小决定了流经工作轮的环流流量的大小，即

v_z=Q/A （13-4）

式中 Q——流过工作轮的液体流量（m³/s）；

A——循环圆内任一截面处的有效通道截面积（m³）。

确定投影v_u的正负号规则应和确定w的正负号的规则相适应，因而从右到左为正，反之为负；投影v_z由里向外为正，反之为负。

从速度三角形又可得

w=v_z/sinβ （13-5）

v_u=u-v_zctgβ （13-6）

v²=v²_z+v²_u （13-7）

而工作轮叶片中任一点的圆周速度（牵连速度）u可用下式求得

式中 r_i——工作轮流道中任一点到轴心的半径；

n——工作轮每分钟转数。