伯努利方程在流体力学中的应用

伯努利方程是能量守恒定律在流体力学中的表达形式。

1.理想液体的伯努利方程

在理想液体的恒定流动中，任取两截面A₁和A₂，如图2-10所示。设截面A₁处的平均流速为v₁，压力为p₁，位置高度为h₁；截面A₂处的平均流速为v₂，压力为p₂，位置高度为h₂。由理论推导可得到理想液体的伯努利方程为

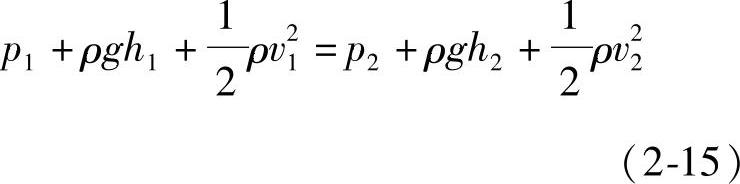
或写成

上式各项分别代表单位体积液体的压力能、位能和动能（或称比压能、比位能和比动能）。

式（2-16）表明，理想液体作恒定流动时，在同一流束内，任意截面上的三种能量可以互相转换，但总和不变。

(www.xing528.com)

图2-10 伯努利方程示意图

2.实际液体的伯努利方程

实际液体是有粘性的，流动时产生内摩擦力而消耗部分能量；同时，管道局部形状和尺寸的骤然变化使液流产生扰动，也要消耗能量。因此，实际液体流动时存在能量损失。另外，在推导理想液体伯努利方程时，认为任取微小流束通流截面的速度相等，而实际液体的粘性使流束在通流截面上各点的真实流速是不相等的。因此，用平均流速计算动能时，必然会产生误差。为了修正这个误差，需引入动能修正系数α。因此，实际液体的伯努利方程为

式中 Δp_w——液体从一个截面运动到另一个截面时，单位体积液体因克服内摩擦力而损失的压力能；

α₁，α2——动能修正系数，当湍流时取α=1，层流时取α=2。

伯努利方程是流体力学的重要方程。在液压传动中，常与连续性方程一起应用来求解液压系统中的压力和速度问题。