经济类管理类联考·海滨逻辑：左撇子与聪明人群比例的探讨

相对数和绝对数问题是日常逻辑中最为精彩的内容之一，原因不仅在于题目难度较大、容易出错，更在于此类问题在日常生活中大量使用，同时错误比比皆是。几乎绝大多数人对这一问题的理解都是有误的，极少有人能够对这类问题有着清晰的思路和较为准确的分析。

下面运用一个典型的例子来做一个详细的剖析，以使大家能够清楚地了解其中的奥秘，便于以后举一反三、灵活运用，应对生活中众多此类问题。在历年联考逻辑真题中，经常会出现一些编写出错的题目，其中在此处出现错误的题目数量最多，在本节列举其中的2道加以详细剖析，以便能纠正所有考生在此之前对此题的误解，能更加深刻地认识和理解此类问题。

在分析此类问题之前，考生可以先认真分析下面这道例题，看是否能够作出准确的分析和判断。

例4-45 （2002-1-23）左撇子的人比右撇子的人更容易患某些免疫失调症，如过敏。然而，左撇子也有优于右撇子的地方，例如，左撇子更擅长于由右脑半球执行的工作。而人的数学推理的工作一般是由右脑半球执行的。

从上述断定能推出以下哪个结论？

Ⅰ.患有过敏或其他免疫失调症的人中，左撇子比右撇子多。

Ⅱ.在所有数学推理能力强的人当中左撇子的比例，高于所有推理能力弱的人中左撇子的比例。

Ⅲ.在所有左撇子的人中，数学推理能力强的比例，高于数学推理能力弱的比例。

A.仅Ⅰ B.仅Ⅱ C.仅Ⅲ D.仅Ⅰ和Ⅲ E.Ⅰ、Ⅱ和Ⅲ

【解析】 在解析这类问题之前，先来学习一个分析模型——相对数、绝对数分析模型，这是笔者潜心多年总结出来的一个极为简单的问题分析模型，可以帮助考生快速分析清楚此类问题。

例如，当我们想知道是左撇子还是右撇子更聪明的时候，做了一个统计调查发现“绝大多数聪明者都是右撇子”，如高达90%，而左撇子只有10%，如图4-2所示。因此，就得出一个结论，认为右撇子更聪明。请问，结论对吗？为什么？

显然，这个结论是不可接受的，我们不能因为右撇子占了聪明人群的绝大多数，就认为右撇子更聪明。因为，很可能右撇子本来人就多，占了人口的绝大多数，这样在聪明人群中右撇子的比例高也就很正常了。

刚才“90%”与“10%”的比较，而得出结论右撇子聪明，这种比较的是“绝对数”，这种比较方式是错误的。而正确的思路是比较“相对数”。

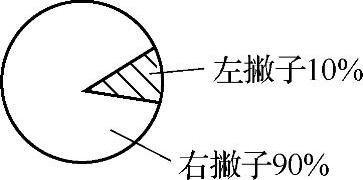
图4-2 总聪明人口中左、右撇子所占比例

即比较之间，哪个“比值”大？这时比较出来的结果是：“每一百个左撇子里有几个聪明的？”与“每一百个右撇子里面有几个聪明的？”谁的数值大，谁就更聪明，这是正确的分析思路。但是，这种计算方式在现实中比较复杂，很难分析清楚，因此在考试中并不可行。为此，引入一个更简单实用的定性分析模型。

当统计调查发现右撇子人占了聪明人群的90%时，是判断不出来左撇子还是右撇子人更聪明的，因为右撇子可能本来就很多，占了人口的绝大多数。这时需要知道一个最关键的信息，那就是“总人口”中“右撇子”的比例是多少？此处有个重要的分析技巧，就是一定要首先假设其比例等于前面给出的“比例”，将90%作为分界点，即假设全部人口中右撇子的比例恰好是90%，接下来分别比较三种情况。如图4-3所示。

图4-3 左、右撇子聪明比例比较

第一种情况，如果总人口中右撇子的比例恰好是“90%”。这就意味着：右撇子占了全部人口的90%，然而在聪明人群中，他也占了90%，恰好等于正常比例，这说明没有差别。此时，可以得出结论，左、右撇子的聪明程度没有差别，进而可以严格证明“聪不聪明”与“是左撇子还是右撇子”无关。

第二种情况，如果总人口中右撇子的比例大于90%，例如，是95%。这就意味着：右撇子占了全部人口的95%，若左、右撇子聪明程度没有差别的话，那么右撇子在聪明人群中所占的比例也应该是这个正常比例95%。然而，事实上右撇子只占了聪明人群的90%，“低于正常比例95%”，说明偏低。此时，可以得出结论，左撇子更聪明。

第三种情况，如果总人口中右撇子的比例小于90%，例如，是70%。这就意味着：右撇子占了全部人口的70%，若左、右撇子聪明程度没有差别的话，那么右撇子在聪明人群中所占的比例也应该是正常比例70%。然而，事实上右撇子占了聪明人群的90%，“高于正常比例70%”，说明偏高。此时，可以得出结论，右撇子更聪明。(www.xing528.com)

至此，现在可以用一种简单的定性分析方法，准确地判断出相对数和绝对数问题。只要是出现了类似的判断问题，都可以用这个模型进行判断。

利用刚才的分析方法，就可以解决之前的例题了。此题，在所有的书中所给的答案和解析都是C选项。但是，真正的结果是，这是一道错题，无正确答案。

此题为归纳题型，相对数、绝对数考点。

Ⅰ错误，左撇子比右撇子更容易患免疫失调症，并不意味着在免疫失调症患者中左撇子就占了大多数，因为很可能在总人口中，左撇子比例本来就很小，人就很少。其中，“免疫失调症”类似于模型中的“聪明问题”。

Ⅱ错误，其意思为，这是错误的。正确的思路是只能，即只能比较“每一百个左撇子里面有几个数学推理能力强的？”与“每一百个右撇子里面有几个数学推理能力强的？”看谁的数值大，谁大谁的数学推理能力就强。

Ⅲ错误，“在所有左撇子的人中，数学推理能力强的比例，高于数学推理能力弱的比例。”

其意思就是左撇子人中，数学推理能力强的人要多于弱的人。这是无关的，左撇子数学推理能力到底强不强？不是跟自己比较，而是与右撇子比较。根据前面的模型分析，正确的思路是比较，即只能比较“每一百个左撇子里面有几个数学推理能力强的？”与“每一百个右撇子里面有几个数学推理能力强的？”看谁的数值大，谁大谁的数学推理能力就强。

所以，通过上述分析，可以发现Ⅰ、Ⅱ和Ⅲ都不对，故在五个选项中并无答案，因此，此题是一道编写错误的题目。但是，在其他教材中，此题都解释为C选项，致使十多年来几乎所有的考生都对此题有误解，形成了错误的思维方式。

【无正确答案】

例4-46 （2009-10-37）据某国卫生部门统计，2004年全国糖尿病患者中，年轻人不到10%，70%为肥胖者。这说明，肥胖将极大地增加患糖尿病的危险。

以下哪项如果为真，将严重削弱上述结论？

A.医学已经证明，肥胖是心血管病的重要诱因

B.2004年，该国的肥胖者的人数比1994年增加了70%

C.2004年，肥胖者在该国中老年人中所占的比例超过60%

D.2004年，该国年轻人中的肥胖者所占的比例，比1994年提高了30%

E.2004年，该国糖尿病的发病率比1994年降低了20%

【解析】 其他书中都将此题解析为C选项。但是，C选项并不构成削弱，属于无关项，此题五个选项中并无正确答案。

根据前面模型例子分析，肥胖者占了糖尿病患者中的70%，并不能说明任何问题，要判断肥胖到底是否增加了患糖尿病的风险，还需要知道肥胖者占全部人口的比例是多少。如果肥胖者占了全部人口的70%，那么是正常比例，这可以说明肥胖和糖尿病并没有关系。如果肥胖者占了全部人口的60%，而糖尿病患者中却占到70%，说明明显偏高，高于正常值（60%），则可以说明肥胖者容易患糖尿病。如果肥胖者占了全部人口的80%，而糖尿病患者中却只占到70%，说明明显偏低，低于正常值（80%），这可以说明肥胖者反而更不易患糖尿病。

需要削弱的是“肥胖会增加糖尿病风险”，只要证明肥胖者在全部人口中的比例“不低于70%”即可，然而，没有选项能够从中得出这一信息，故无正确选项。其中，其他教材解释的选项为C选项，是错误的。根据肥胖者占中老年人的60%，根本判断不出肥胖者占全国人口的比例。因此，本题没有正确选项，是一道编写错误的题目。多年来一直给广大考生造成极大的误解，影响了正确思维的形成。

【无正确答案】