经济类管理类联考：海滨逻辑分析

在人们的思维形态中，最基本的思维形式或逻辑关系有九种，通常称为九种思维形式或九种逻辑关系，它是人们认识和感知思维形式的语言工具，是理解形式逻辑最重要的基础。

在“学院派”逻辑学教程中所用的符号为p、q、r、s等，而在本章中所用的符号是更直观和易于理解的A、B、C、D等符号体系。A和B所代表的是关键词出现的先后顺序，先出现的关键词是A，后出现的关键词是B。

传统的“学院派”逻辑学方法非常难学和效果很差的一个重要原因就在于：现有的逻辑学理论中没有对最基本的逻辑关系进行很好的系统总结，并没有把日常生活中常见的能够表示逻辑关系的逻辑连接词进行系统的归纳和整理，所以学生在学完形式逻辑之后还是不知道很多词到底表达的是什么逻辑关系，对逻辑关系的理解就会出现错误，即在形式逻辑题目入手之时就已经出错，导致后续在错误的逻辑关系理解下进行错误的推演，得出错误的结果，根本无法判断出正确的选项，而又不能理解自己错在哪里。所以，九种逻辑关系是理解形式逻辑基础的语言工具，务必背诵和理解清楚，才能为后面形式逻辑的进一步学习打下必要的基础。

■ 九种逻辑关系

九种逻辑关系如表1-2所示。

表1-2 九种逻辑关系

■ 九种逻辑关系解析

1.“且”的逻辑关系

“∧”的逻辑关系是反映若干事物、情况共存的复合命题。它所表达的思维形式含义是“同时成立”，而能够表达这种思维形式的连接词有“但是……”“……并且……”“既……又……”“……同时……”等，符号化时表示为“A∧B”。例如，“A去，但是B不能去”，就表示为：A∧﹁B。

注意，“但是”在言语理解和日常生活中表示“转折”，但是在最基本的思维形式中没有“转折”这种思维形式，“A去，但是B不能去”表示的思维形式就是：A去，同时B不能去。

2.“或”的逻辑关系

“∨”的逻辑关系是反映若干事物情况中至少有一个存在的复合命题。它所表达的思维形式含义是“至少有一个”，而能够表示这种思维形式的连接词有“或者…或者……”“……至少有一个……”等，符号化时表示为“A∨B”。例如，“或者小张去，或者小王去”，就表示为：“小张∨小王”。

A和B的所有组合一共有四种可能性：A∧﹁B、﹁A∧B、A∧B、﹁A∧﹁B。现实中这四种可能性是互斥的，即不能同时出现两个以上的情况，并且它们又是全集，即没有其他的可能性了，所以，现实情况一定是要出现四种可能性中的某一种。而A∨B描述的可能性是其中的前三种可能性：A∧﹁B、﹁A∧B、A∧B。这是一个集合的概念，只知道现实是三种可能性中的某一个出现了，至于到底是哪个情况出现了是无法判断的。

还有一种较为特殊的不相容“”的逻辑关系，是反映若干事物情况只能有一个存在的复合命题。它所表达的思维形式含义是“只能有一个”，而能够表示这种思维形式的连接词有“要么……要么……”“或者……或者……，二者必居其一”等，符号化时表示为“A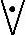B”。例如，“要么小张去，要么小王去”，就表示为：“小张小王”。

A和B的所有组合一共有四种可能性：A∧﹁B、﹁A∧B、A∧B、﹁A∧﹁B。而A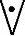B表示的可能性有两种：A∧﹁B、﹁A∧B。

注意：“且”和“或”的逻辑关系无前后之分，即“A∧B”与“B∧A”，“A∨B”与“B∨A”，“A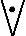B”与“B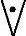A”之间没有任何区别，逻辑含义是完全一致的。

3.“否”的逻辑关系

“﹁”的逻辑关系是否定一个命题的复合命题。它所表达的思维形式含义是“不成立，为假”，而能够表示这种思维形式的连接词有“并非”不同意“……为假”及其他否定词等。

“﹁”的逻辑关系有以下五种形式：

（1）﹁A。例如，并非小王是党员，表示为“﹁小王”。

（2）﹁（A∧B）=﹁A∨﹁B。例如，并非小王和小张都是党员，表示为“﹁（小张∧小王）”，其转换的等价结果是：﹁小张∨﹁小王。

（3）﹁（A∨B）=﹁A∧﹁B。例如，并非小王或小张是党员，表示为“﹁（小张∨小王）”，其转换的等价结果是：﹁小张∧﹁小王。

（4）﹁（A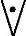B）=（A∧B）（﹁A∧﹁B）。例如，要么小王是党员，要么小张是党员，事实并非如此，表示为“﹁（小张小王）”，其转换的等价结果是：（﹁小张∧﹁小王）（小张∧小王）。即要么都是，要么都不是。

（5）﹁（A→B）=A∧﹁B。对推理取否，即否定推理，推理为假。例如，如果你赢了，就给你100元钱，事实并非如此。表示为“﹁（赢了→给钱）”。其转换的等价结果是：赢了∧﹁给钱。即“只要你赢了就给你100元钱”这句话在“赢了同时没有给钱”出现的情况下才为假话，本知识点将在三大理论基石一中加以证明。而对于后推前的情况只需把“A←B”变成“B→A”，与上述情况完全一致，此处不再赘述。

4.“前推后”的逻辑关系

能够表示“前推后”的连接词有两类：一类是假设；另一类是现实。假设，即逻辑学中的假言命题，是反映两个事物情况条件关系的复合命题。例如，只要明天下雨，就取消运动会。现实，即逻辑学中的直言命题，是对现实情况的一种判断，无需满足某些条件。例如，所有同学都是党员。

因此，“→”的逻辑关系是反映前面事物情况是后面事物情况充分条件的假言命题，又可以反映对一个事实的判断。但是，二者共有的思维形式含义是“前面成立，则后面一定会成立”，而能够表示这种思维形式的连接词常见的有五个，并且分为假设和现实两类。假设类有：“……必须……”“如果……那么……”“只要……就……”等。现实类有：“……是……”“所有……都……”等。其符号化时结构都为“A→B”。例如，如果明天不下雨，我就去听音乐会，就表示为：﹁下雨→听音乐会。

“……必须……”这个连接词是在试题中经常出现的高频词，但是它真正表示的逻辑关系是充分条件，即“前推后”，而不是“后推前”，而绝大多数考生对此一直存在误解，教材中也没有给出分析和总结，是一个容易理解错误的连接词。

例如，“活着必须呼吸”。如果假设这句话是正确的，那么就意味着：有一个活着的人，一定能够判断出他在呼吸。所以“活着必须呼吸”这句话蕴含的思维形式是“活着→呼吸”，即“前推后”的思维形式，而决定这种思维形式的连接词就是“必须”，所以，必须牢记这个易错连接词的逻辑关系。

“如果……那么……”“只要……就……”这两个常见的连接词在几乎所有的逻辑教材中都有阐释，表示的逻辑关系都是“前推后”，符合思维习惯，也很少被误解。

“……是……”“所有……都……”这两个连接词在逻辑教材中被称为直言命题，就是反映对象具有或不具有某种性质的简单命题。在语言中，通常用“……是……”和“……不是……”来描述事物是否具有某种性质，在很多逻辑教材中也未对该词的逻辑关系进行系统分析，也是一个比较容易误解的连接词。而“所有……都……”和“所有……都不……”与前面的“……是……”和“……不是……”是相对应的，但它们描述的是“全部事物”是否具有某种性质。

例如，“台湾人是中国人”，假设这句话是正确的，那么就意味着：有一个台湾人，一定能断定他是中国人。所以“台湾人是中国人”这句话蕴含的思维形式为“台湾人→中国人”，即台湾人具有中国人的性质。而“美国人不是中国人”描述的是美国人不具有中国人的性质，即假设这句话是正确的，那么就意味着：有一个美国人，一定能断定他不是中国人。所以这句话蕴含的思维形式为“美国人→﹁中国人”。

注意：“是”这个连接词蕴含的思维形式为“前推后”。但是，因果关系时除外，在这时只能用因果关系来判断。例如，“飞机失事的原因是飞行员操作失误”，这句话的因果关系为“失误→失事”。

除了上述常见的五个表示“前推后”的连接词之外，还有很多时候会出现没有连接词的情况，对这种“无连接词”情况的处理是：判断因果关系或推理关系。能够识别出因果关系时，即蕴含的思维形式为“因→果”，例如，“飞机失事的原因是飞行员操作失误”，这句话中蕴含的思维形式为“失误→失事”。能识别出推理关系时，一般也可以写出“前推后”的形式，例如，“公正分配将结束经济风险”，假设这句话是正确的，那么就意味着：公正分配一旦出现，经济风险就没有了。通过这种描述推理关系的语句，可以判断这句话的逻辑关系为“公正分配→﹁风险”。

注意：在有连接词的情况下，一定要以连接词的逻辑关系为准，不能按其他方式去理解；而在没有连接词的情况下，才考虑因果关系和推理关系。

5.“后推前”的逻辑关系

“←”的逻辑关系是反映前面事物情况是后面事物情况必要条件的假言命题，描述的是“假设”，而不是“现实”。它所表达的思维形式含义是“前是后的必要条件”，而能够表示这种思维形式的连接词有以下两类：

第一类是“只有……才……”，此外它们单独出现也可以，即“只有……”“……才……”，符号化时表示为“A←B”。例如，“只有好好学习，才能考上大学”，就表示为“好好学习←考上大学”。而不是通常认为的“好好学习→考上大学”，此处很容易被误解，没有接触过逻辑的人基本上都会存在这个误解，这是由于汉语的表达习惯造成的，对这个连接词必须加以纠正。一旦用了“只有……才……”这个连接词，所表达的思维形式就是固定的“后推前”。如果想表达的不是这个意思，那就是连接词用错了，必须要用其他的连接词才行。

第二类是“A是B的必要条件”，类似必要条件的说法还有“先决条件”“前提”“基础”等，符号化时表示为“A←B”。

注意：第二类情况的标准说法是“A是B的必要条件”，所以，在遇到“A是以B为先决条件”的说法时，一定要转换成第二类情况的标准说法“B是A的先决条件”，然后再进行分析。

在解释第二类中的这几个连接词之前，首先了解一下“充分条件”和“必要条件”之间的本质区别是什么？如何来区分和识别这两个概念？它们之间又有什么样的本质联系？

•充分条件和必要条件的本质区别，如表1-3所示。

表1-3 充分条件和必要条件的本质区别

(www.xing528.com)

充分条件与必要条件的本质区别就在于：“前推后”与“后推前”。

（1）如果推理方向“→”成立，就意味着：充分条件成立，即前面是后面的充分条件。

（2）如果推理方向“←”成立，就意味着：必要条件成立，即前面是后面的必要条件。

（3）如果推理方向“→”和“←”都成立，就意味着：充要条件成立。

（4）如果推理方向“→”和“←”都不成立，就意味着：既不充分，又不必要。

例如，考虑“起动”与“驾驶”这两个词之间的逻辑关系，发现“→”不一定成立，所以充分条件不成立，而“←”一定成立，所以必要条件成立，于是就会说“起动”是“驾驶”的必要条件。

•充分条件和必要条件的本质联系，如表1-4所示。

表1-4 充分条件和必要条件的本质联系

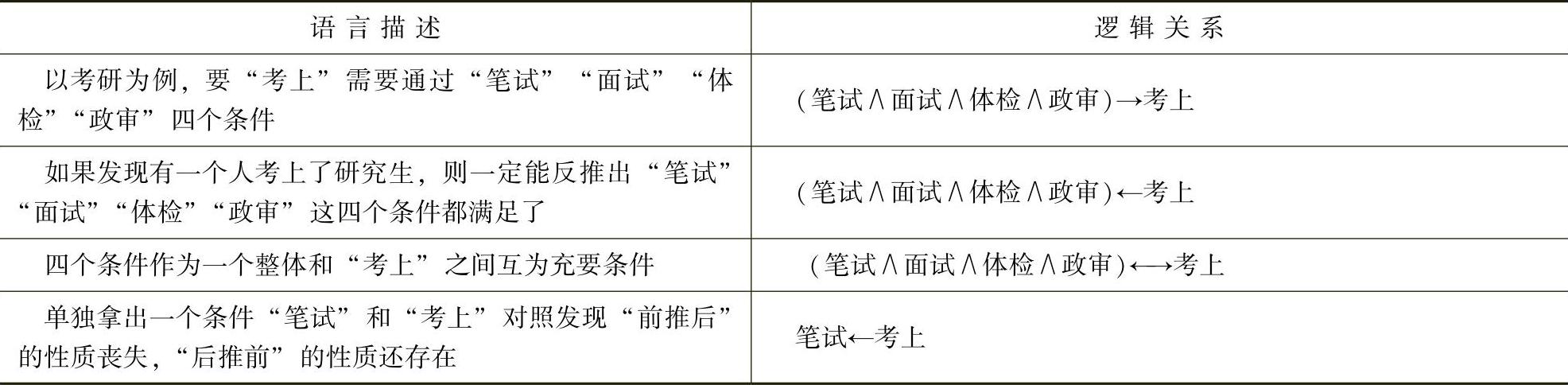
在日常生活当中，通常会说“通过笔试是考上研究生的必要条件”，“通过笔试是考上研究生的先决条件”，“通过笔试是考上研究生的前提”，“通过笔试是考上研究生的基础”，所以在题目中见到“A是B的必要条件（先决条件、前提、基础）”的说法时，逻辑关系就是“后推前”。

充分条件与必要条件的本质联系就是：所有必要条件合在一起就等于充分条件。

考上研究生的必要条件有四个（笔试、面试、体检、政审），单独拿出某几个条件都不行，必须所有必要条件都满足时方能推出考上研究生了，即“所有必要条件合在一起就等于充分条件”。

例1-1 （2004-1-42）许多国家首脑在出任前并未有丰富的外交经验，但这并没有妨碍他们作出成功的外交决策。外交学院的教授告诉我们，丰富的外交经验对于成功的外交决策是不可缺少的。但事实上，一个人，只要有高度的政治敏感、准确的信息分析能力和果断的个人勇气，就能很快地学会如何作出成功的外交决策。对于一个缺少以上三种素养的外交决策者来说，丰富的外交经验没有什么价值。

如果上述断定为真，则以下哪项一定为真？

A.外交学院的教授比任前的国家首脑具有更多的外交经验

B.具有高度的政治敏感、准确的信息分析能力和果断的个人勇气，是一个国家首脑作出成功的外交决策的必要条件

C.丰富的外交经验，对于国家首脑作出成功的外交决策来说，既不是充分条件，也不是必要条件

D.丰富的外交经验，对于国家首脑作出成功的外交决策来说，是必要条件，但不是充分条件

E.在其他条件相同的情况下，外交经验越丰富，越有利于作出成功的外交决策

【解析】 只要有三种素养，没有外交经验也可以成功，这说明“﹁经验→﹁成功”不成立，那么等价逆否“经验←成功”同样也不成立，即“后推前”不成立，意味着必要条件不成立。缺乏三种要素，有外交经验也不一定成功，这说明“经验→成功”不成立，即“前推后”不成立，意味着充分条件不成立。因此，经验对成功来说，既不是充分条件，也不是必要条件，故C选项正确。

【正确答案为C】

充分条件和必要条件是两个非常重要的概念，不仅因为它们在逻辑试题中会经常出现，而且它们与我们的日常生活高度相关。在日常生活中我们经常用到充分条件和必要条件这两个概念，然而几乎没有人能够把这两个概念的本质区别与联系理解清楚、区分清楚、解释清楚。因此，导致充分条件和必要条件这两个概念久攻不下，希望考生以后能够对这两个概念融会贯通。

“前推后”和“后推前”是九种逻辑关系中最重要的两种逻辑关系，因为在形式逻辑考题中，能表示为这两种基本逻辑关系的题目很多。

注意：“→”和“←”的逻辑关系是有前后之分的，即“A→B”与“B→A”，“A←B”与“B←A”之间是有本质的区别的，逻辑含义完全不一样，因此不能随意变换位置。

6.“互推”的逻辑关系

“A←→B”的逻辑关系是针对“当且仅当，A是B的唯一必要条件”这两个连接词的。它表示“充要条件的关系”，也就是前推后和后推前同时成立的情况，有一些连接词可以直接表达出这种逻辑关系。

“A出现，当且仅当B出现”这是一种固定表达形式，即“A←→B”。而“A是B的唯一必要条件”可以通过前面的知识拆解出来，首先看“A是B的必要条件”这种说法，其逻辑关系是“A←B”，再看“唯一必要条件”，前面讲过“所有必要条件合在一起就等于充分条件”，既然是“唯一必要条件”，那么这一个条件已经是所有必要条件，那么就可以构成充分条件，“A→B”成立。故两个推理方向同时成立，可以写成“A←→B”。

7.“A推否B”的逻辑关系

“A→﹁B”的逻辑关系主要针对“没有（一个）A是B”这个连接词，描述的是“现实”，而不是“假设”。它表示的是“所有的A都不是B”。例如，“没有一个同学喜欢他”的含义是“所有同学都不喜欢他”，因此，逻辑关系应该是“同学→﹁喜欢”。而不是“﹁A→B”，“﹁A→B”逻辑关系的“现实”含义是“否A推B”，即“非同学的人都喜欢他”，也就是“除同学之外”的人都喜欢他。

8.“否A推B”的逻辑关系

“﹁A→B”的逻辑关系是针对“除非……否则……”这个连接词所设立的，描述的是“假设”，而不是“现实”。它表示“在A不成立的情况下，一定会有B情况出现”。“除非……否则……”是日常生活中经常用到的一个连接词，但是我们对这个词的理解只是停留在“语意理解”的层面上，而没有从“思维形式”的层面去理解。因此，“除非你去，否则我不去”这句话我们可能会理解清楚其含义，而“除非你去，否则我去”这句话我们就无法理解了，因为在日常生活中从来没有这么说过，琢磨不清楚它的含义。

而海滨逻辑最主要的一个出发点就是要从语意出发去理解众多思维形式，直接读懂其思维形式或逻辑结构，简单易懂，便于记忆和理解。其实，在“除非你去，否则……”这句话中，应注意理解“除非你去，否则……”中的“否则”，它到底是在否谁？它到底指什么情况？其实，“否则”是在否“你去”的情况，是说：在“你不去”的情况下，“否则”后面的情况一定会出现。所以，从意思理解的角度，分析清楚其逻辑关系为“﹁A→B”。还有一种倒置的说法是“B，除非A”，注意，我们始终将“除非”后面的视为A，因此逻辑关系还是“﹁A→B”。

“除非A，否则B”这个逻辑关系，在国内外所有逻辑学书中都表示为“﹁B→A”，这个逻辑关系虽然是正确的，与“﹁A→B”是等价的逆否命题。但是，这个逻辑关系的表示方法是无法从“除非……否则……”这个词的字面意思上理解的，所以字面语义与思维形式相脱节，因此，在记忆“﹁B→A”就必须死记硬背，不利于应用而且会很容易遗忘。如果按“﹁A→B”这个逻辑关系理解则会解决上述理解和记忆的难题。

9.“有A推B”的逻辑关系

“有A→B”是一种极为特殊和重要的逻辑关系。其一，在所能见到的逻辑教材中从未有过这种逻辑关系的表示方法，这种逻辑关系是笔者自创的一种表示方法。其二，这种逻辑关系有三个鲜为人知的重要特性，即使知道其中某些特性，也无法知晓如何在题目中运用。

“有A→B”表示的逻辑含义是“存在性判断”，即“存在这样的A是B”。能够表示这种逻辑关系的连接词有“有的……是……”“一些……是……”“有些……是……”等。其中“有的”“一些”“有些”这些连接词被称为“不定量词”，表示数量不确定的词。例如，有的同学是党员，就表示为“有的同学→党员”；一些同学是党员，就表示为“一些同学→党员”。不定量词的“不确定”体现在两个方面：①数量不确定；②是谁不确定。例如，有的同学是党员，我知道有这样的同学，但是，数量不确定，范围在：1→全部。具体有几个是不知道的。是谁也不确定，我只知道有同学是党员，是张三吗？是李四吗？不确定。

■ “有A→B”的三个重要特性

（1）两个不确定：①数量不确定（范围：1→全部）；②是谁不确定。例如，有的同学是党员。我只知道有这样的同学，但是有几个不知道，可能是一个，也可能是两个，也可能是全部。所以“有的”的范围是“1→全部”，是变动的，现实情况具体是什么并不知道。另外，只知道有同学是党员，但“是谁不确定”。

在“A→B”的逻辑关系中，A前面省略的量词是“所有”，即表示“所有的A都是B”。而在“有A→B”的逻辑关系中，A前面出现的是一个范围不确定的不定量词“有的”，即表示“存在A是B”，但是具体数量是多少不确定，只知道其范围是“1→全部”。

（2）不能取逆否（即﹁B→…A是错的）。由于在“有A→B”中，A前面有一个范围不确定的不定量词，所以与“A→B”相比较，它丧失了一个非常重要的逆否特性，即从﹁B反推不出任何信息，这个需要考生高度注意，一旦有选项取逆否之后进行反推，那么该选项一定是错误的。

（3）有A→B=有B→A（海滨互换特性）。这是一个极为重要的特性，了解和灵活运用此特性，能够破解所有的欧拉图解法题目。现在可以用简单而又严格的推理去证明之前必须用欧拉图解法才能分析清楚的题目，这是笔者在做欧拉图解法题目时的一个重要发现和应用。

图解证明：“有的A是B”如果为真，那么就意味着A和B一定是有交集的，即相交的那部分的A是B，此时，反问“有的B是A”是否正确，则也一定是正确的，因为相交的那部分的B是A，如图1-1所示。

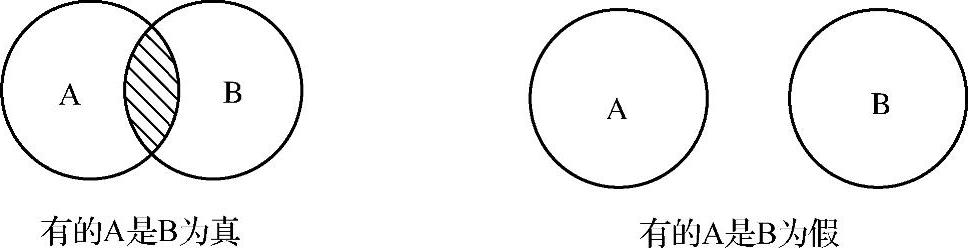
图1-1 图解