1991年美国克罗拉多大学的T.H.Wu等由州公路局支持在室内建造了分层布筋的加筋土挡墙,进行足尺模型试验。该模型墙即称Denver墙,包括一个黏性土挡墙和砂土挡墙。Wu等公布试验原始数据,让人们预测模型挡土墙的受力变形和破坏情况,以验证和评价土工织物加筋土的计算方法,进一步了解加筋土体的受力变形性质,推动加筋土建筑物的设计和建造[141~143]。
7.3.1 Denver墙试验介绍
7.3.1.1 挡土墙尺寸和加载装置
模型墙高10ft(304.8cm),长6ft10in(208.3cm),宽4ft(121.9cm)。加筋层数为12层,除最低层间距为7in(17.8cm)外,其他各层间距均为11in(27.9cm)。最低和最顶层的布筋长度为6ft6in(198.1cm),其他各层均为5ft6in(167.6cm),折返段长度3ft(91.4cm)。Denver墙几何尺寸和土工织物的布置方式见图7.3.1和图7.3.2(为尊重原始资料,图中所用单位均为原始资料中的单位),注意底部7in厚为砂层,其他各层填料为砂(砂土挡墙)或黏土(黏性土挡墙)。墙体加载通过装在顶部的气囊进行,在气囊和墙顶之间铺一层2ft(61.0cm)厚的砂垫层,以保证传到墙顶的力能够均匀分布。模型槽的侧板刚度和侧壁的润滑处理经试验验证能够满足平面应变的要求。在模型装置的底板上粘一层粗粒料,使墙体建在粗糙底面上。
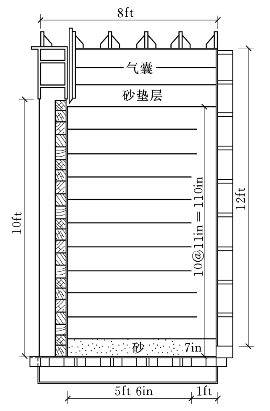
图7.3.1 Denver墙的几何尺寸(1ft=30.48cm,1in=2.54cm)

图7.3.2 土工植物的布置方式(1ft=30.48cm,1in=2.54cm)
7.3.1.2 施工顺序和加载过程
图7.3.3所示的是加筋土挡墙的施工过程。挡土墙面板采用木面板,面板之间用0.5in(1.3cm)厚的胶合板连接。除了在用销钉连接面板时作了必要的保护外,整个施工过程中没有临时支撑。
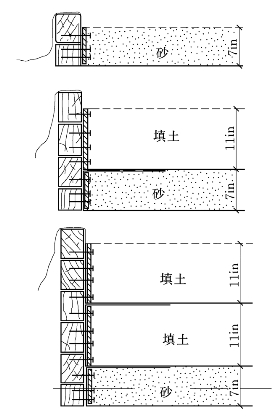
图7.3.3 Denver墙的施工顺序(1in=2.54cm)
墙体建造完成后,墙顶铺上2ft(61.0cm)厚的砂垫层。然后通过气囊施加均布荷载。荷载每级3psi(20.7kPa),直 到15psi(103.4kPa)。每级荷载之间的时间间隔为30min。达到15psi时保持100h荷载不变,观察墙的蠕变情况。此后继续以3psi的荷载增量,分级加载,直至破坏。注意上述荷载都包括了墙顶部气囊下砂垫层的重量。
7.3.1.3 试验内容
先做加筋砂土挡墙试验。在从27psi(186.0kPa)向30psi(206.7kPa)加载的过程中墙体变形显著增加,29psi(199.8kPa)时气囊爆破。换上新气囊加压,27~29psi之间变形显著。
至于加筋黏性土挡墙,30~33psi时变形加剧,33psi(227.4kPa)时气囊爆破。换上新气囊,34psi(234.3kPa)时气囊又破坏,试验终止。
试验过程中分别量测了挡土墙的顶部沉降、面板的侧向位移以及土工布中的应变。其中土工布中的应变选择3个不同高度:0.15H、0.52H、0.88H(H=120in=304.8cm)分别进行量测。
7.3.2 用NMFRS程序计算Denver墙
程序NMFRS是介玉新开发的有限元计算程序,可用于计算一般挡土墙、边坡,也可以计算加筋挡土墙或边坡,可以用常规方法计算,也可以用等效附加应力法计算加筋土问题。
程序中计算土单元的模型可根据情况选用多重势面模型、线弹性模型或邓肯—张模型(E—B模型或E—μ模型)。界面单元用Goodman模型,筋材模拟成只能受拉不能受压的杆单元。当筋材受拉时,杆单元模量可根据筋材拉伸试验求得。假设拉伸试验中单位宽度拉力T与筋中应变ε的关系为:
T=Aεr
其中A、r为试验参数,那么杆单元模量E与筋材厚度h乘积为:
Eh=Arεr-1
杆单元的模量随应变ε的变化而改变。当杆单元受压时,取其模量为一小值。
采用两种方法(常规方法、等效附加应力法)、两种模型(E—μ模型、多重势面模型)计算Denver墙。此处只给出多重势面模型和E—μ模型采用常规方法的计算成果。
7.3.2.1 材料参数
土单元采用E—μ模型和多重势面模型,界面单元用Goodman模型,筋材模拟成只能受拉不能受压的杆单元。根据试验原始资料可确定材料参数如下:
(1)砂土。根据三轴试验资料求出参数,见表7.3.1。注意其中G=0.8>0.5,E—μ模型已不适用,只能用多重势面模型。用表7.3.1中的参数反算砂土的应力应变关系曲线,结果见图7.3.4。可见多重势面模型能较好地反映土的剪胀性。
表7.3.1 砂土的模型参数

注 1psi=6.89kPa,1pcf=0.1571kN/m3。
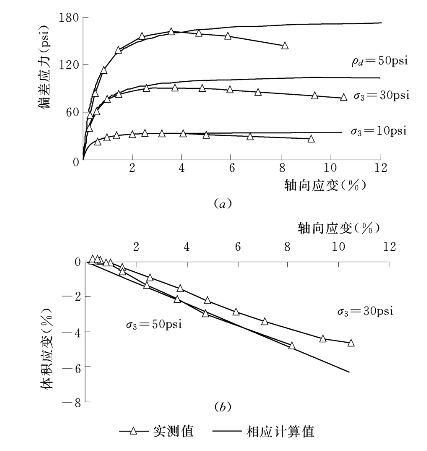
图7.3.4 砂土三轴试验计算值(多重势面模型)与实测值比较(https://www.xing528.com)
(2)黏性土。根据试验成果整理的有关参数如表7.3.2所示:
表7.3.2 黏性土的模型参数

注 1psi=6.89kPa,1pcf=0.1571kN/m3。
(3)面板。面板参数取:
E=1987psi=13690kPa,μ=0.3,厚度取4.6in(11.7cm)。
(4)筋材。假设土工布单位宽度拉力与应变关系为:
![]()
根据土工布的拉伸试验结果,取:A=1059lb/ft=88.25 lb/in=15.4kN/m,r=0.66。计算中不考虑筋材的蠕变效应。
(5)界面性质。界面单元采用Goodman模型。根据直剪试验资料可求出砂土—筋和黏土—筋界面参数指标,见表7.3.3所示。
表7.3.3 界面参数
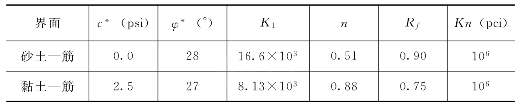
注 1psi=6.89kPa,1pcf=0.1571kN/m3。
7.3.2.2 计算成果
土和面板模拟成四节点等参元,筋材(土工布)模拟成只能受拉不能受压的杆单元,在土和筋材之间设Goodman界面单元。计算网格如图7.3.5所示。节点总数438,单元总数516:其中土单元143,面板单元11,杆单元125,界面单元237。土单元网格共分11层,最低一层高7in(17.8cm),其余各层高度均为11in(27.9cm)。墙体底部为铰支座,墙背为辊轴支座。在折返段筋的重叠部分杆单元的模量加倍。
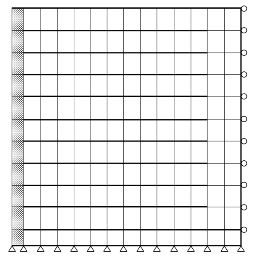
图7.3.5 有限元网格
计算分4个分期:
第一期:填筑到高度51in(129.5cm)
第二期:填筑到84in(213.4cm)
第三期:填筑到117in(297.2cm)
第四期:施加上覆荷载到15psi(103.4kPa)—分5级加载,每级3psi(20.7kPa)
(1)加筋砂土挡墙的计算。土的参数见表7.3.2,由于砂土的泊松比μ>0.5,无法用E—μ模型计算,所以只选用多重势面模型计算砂土挡墙。
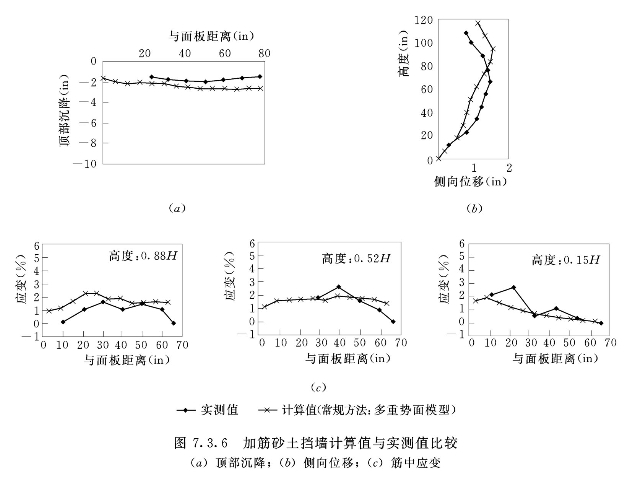
15psi时墙顶沉降计算结果与实测值比较见图7.3.6(a),面板侧向位移计算与实测值的比较见图7.3.6(b)。注意这些位移都扣除了填筑完成时的位移,即图中给出的是单纯由外荷引起的墙体的变形。
可以看出计算和实测结果还是比较接近的,但是与实测值相比,计算的顶部最大沉降位置更靠右端。造成这种差别的原因可能是有限元计算中墙体右端节点的约束采用辊轴支座,限制其水平向位移而不限制竖向位移,即相当于假定墙背与模型槽壁为光滑接触。而实际上两者之间是有摩擦作用的。
0.15H、0.52H、0.88H(H=120in=304.8cm)处筋中应变计算值与实测值的比较见图7.3.6(c)。
(2)加筋黏性土挡墙的计算。分别用E—μ模型和多重势面模型计算黏性土挡墙。
1)用E—μ模型计算。15psi时墙顶沉降及面板侧向位移的比较见图7.3.7(a)、(b)。图中的位移值同样扣除了填筑完成时的位移,给出的是单纯由外荷引起的墙体的变形。0.15H、0.52H、0.88H处筋中应变计算值与实测值的比较见图7.3.7(c)。同砂土挡墙的计算结果类似,位移分布与实测结果有一定差别。这些同样可能是由边界条件引起的。
2)用多重势面模型计算。图7.3.7中同时给出了多重势面模型的相应计算成果。从图中可以看出,多重势面模型和E—μ模型的计算结果是非常接近的,只是多重势面模型的计算值略小。

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




