高双刚性墙方案（DHHW）及其土的本构模型应用

高双刚性墙方案先建下游墙，后建上游墙，墙厚1.2m，应用以上各种本构模型对围堰及防渗墙的受力计算结果如下。

（1）墙体水平位移。各种本构模型计算的墙体上、下游墙的水平位移如图6.5.1所示，最大水平位移如表6.5.1所示。

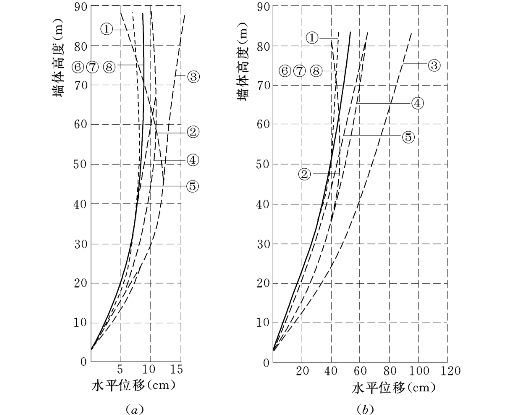
图6.5.1 高双刚性墙不同本构模型计算的墙体位移

（a）上游墙；（b）下游墙
①—E-μ；②—DS—E—μ；③—E-B（μ≥0.1）；④—E—B（μ≥0.25）；⑤—E—B（μu=0.333）；⑥—EP—E—μ；⑦—EP—E—B（μ≥0.1）；⑧—EP—E—B（μ≥0.25）

表6.5.1 高双刚性墙方案各种本构模型计算的墙体最大水平位移值

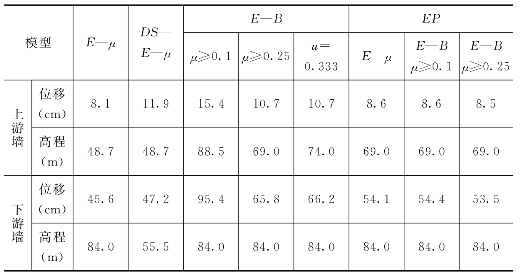
由表可见，一般E—B模型计算出的水平位移最大，E—μ模型最小，与上面结果一样，μ值小的模型位移大。略去偏大的E—B模型，则上游墙最大位移约8.5cm，下游墙最大位移约50cm左右。

（2）墙体垂直应力σy。上、下游墙的上、下游侧不同的本构模型计算得到的σy分布如图6.5.2～图6.5.5所示，由图可见，在墙底端处，弹塑性模型的σy值最小，受力状态最好。

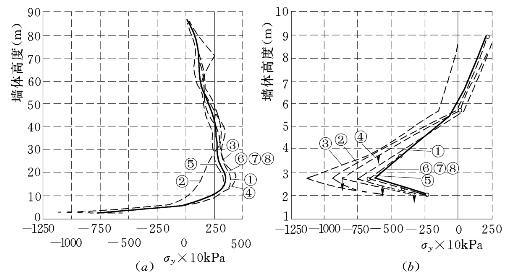
图6.5.2 高双刚性墙上游墙上游侧σy

（a）σy沿墙高分布；（b）墙底端σy放大图
①—E-μ；②—DS—E—μ；③—E-B（μ≥0.1）；④—E—B（μ≥0.25）；⑤—E—B（μu=0.333）；⑥—EP—E—μ；⑦—EP—E—B（μ≥0.1）；⑧—EP—E—B（μ≥0.25）负为拉应力 正为压应力

图6.5.3 高双刚性墙上游墙下游侧σy

（a）σy沿墙高分布；（b）墙底端σy放大图
①—E-μ；②—DS—E—μ；③—E-B（μ≥0.1）；④—E—B（μ≥0.25）；⑤—E—B（μu=0.333）；⑥—EP—E—μ；⑦—EP—E—B（μ≥0.1）；⑧—EP—E—B（μ≥0.25）负为拉应力 正为压应力

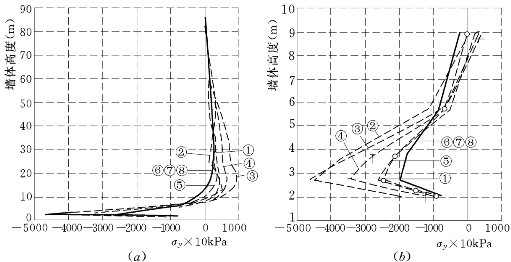
图6.5.4 高双刚性墙下游墙上游侧σy

（a）σy沿墙高分布；（b）墙底端σy放大图
①—E-μ；②—DS—E—μ；③—E-B（μ≥0.1）；④—E—B（μ≥0.25）；⑤—E—B（μu=0.333）；⑥—EP—E—μ；⑦—EP—E—B（μ≥0.1）；⑧—EP—E—B（μ≥0.25）负为拉应力 正为压应力

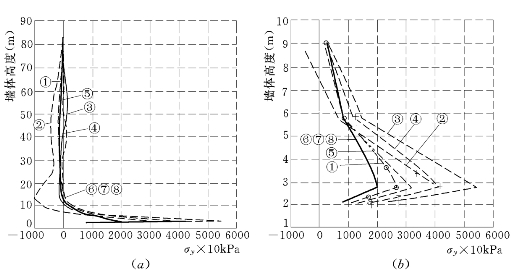
图6.5.5 高双刚性墙下游墙下游侧σy

（
a）σy沿墙高分布；（b）墙底端σy放大图
①—E-μ；②—DS—E—μ；③—E-B（μ≥0.1）；④—E—B（μ≥0.25）；⑤—E—B（μu=0.333）；⑥—EP—E—μ；⑦—EP—E—B（μ≥0.1）；⑧—EP—E—B（μ≥0.25）负为拉应力 正为压应力

（3）墙体单元破坏情况。不同的本构模型墙体的破坏单元数如表6.5.2所示，主要破坏单元在墙的底部，且破坏单元多数为拉坏，同时先建的下游墙出现的破坏数多于后建的上游墙的破坏单元数。图6.5.6、图6.5.7给出了E—μ模型和EP—E—μ模型墙体破坏单元的位置。因此，破坏单元数以弹塑性模型最少。

表6.5.2 高双刚性墙不同模型计算的墙体破坏单元数

(www.xing528.com)

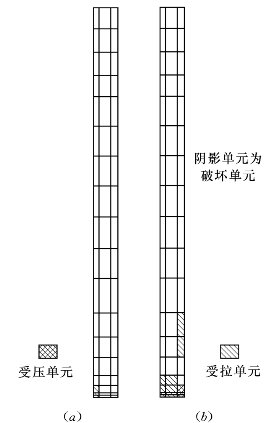
图6.5.6 高双刚性墙方案E—μ模型上、下游墙破坏单元的位置

（a）上游墙；（b）下游墙

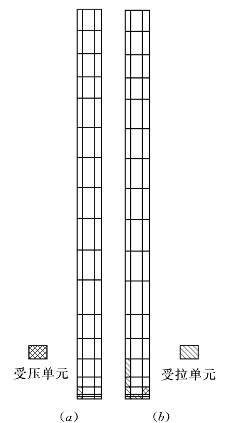
图6.5.7 高双刚性墙方案EP—E—μ模型上、下游墙破坏单元的位置

（a）上游墙；（b）下游墙

（4）堰体的沉降、水平位移及应力水平。不同本构模型计算的堰体最大沉降及水平位移的位置有所不同，且不同模型结果也相差较大，如表6.5.3所示，以E—B模型最大，其他各种模型较为接近。

表6.5.3 不同模型计算的堰体最大沉降及水平位移

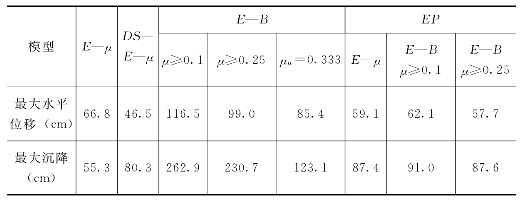
图6.5.8～图6.5.11给出E—μ模型和EP—E—μ模型的堰体沉降、水平位移等值线，图6.5.12、图6.5.13给出了E—μ模型和EP—E—μ模型的堰体应力水平等值线图，由图可见，最大应力水平位于上游墙的上游侧，这是由于水压力作用使墙体侧移，土体侧向应力减少造成该区应力水平较高，是合理的。堰体破坏区范围较小，故堰体是稳定的。

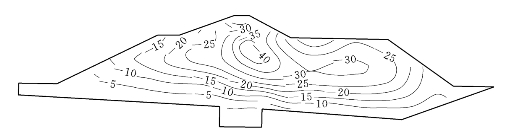
图6.5.8 高双刚性墙方案堰体沉降等值线图（E—μ模型）（单位：cm）

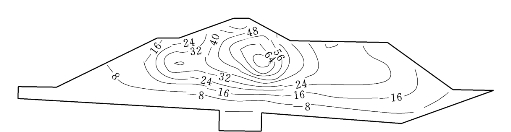
图6.5.9 高双刚性墙方案堰体沉降等值线图（EP—E—μ模型）（单位：cm）

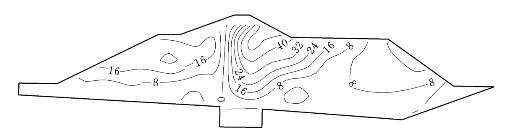
图6.5.10 高双刚性墙方案堰体水平位移等值线图（E—μ模型）（单位：cm）

图6.5.11 高双刚性墙方案堰体水平位移等值线图（EP—E—μ模型）（单位：cm）

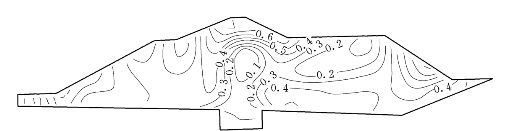
图6.5.12 高双刚性墙方案堰体应力水平等值线图（E—μ模型）

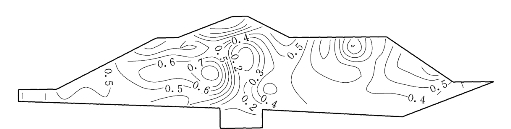
图6.5.13 高双刚性墙方案堰体应力水平等值线图（EP—E—μ模型）

（5）小结。高双刚性墙是先建下游墙，后建上游墙的，与以上的低双墙方案的施工顺序是相反的，故墙体位移大的是下游墙，受力大、破坏单元多的也是下游墙。各种不同的本构模型中，无论是墙体水平位移还是堰体的位移，均是E—B模型较大，E—μ模型较小，与上面结果是一致的。除E—B模型较大外，其他模型平均值大致为：上游墙的水平位移约8.5cm，下游墙的水平位移约50cm，墙体的应力状态以弹塑性模型最好，墙体破坏单元数以弹塑性模型最少，但这种破坏由于未考虑单元破坏后刚度及应力的重分配，故实际结果是夸大的，但通过不同模型结果比较，证明弹塑性模型还是有其优越性的。