低双刚性墙方案（LDHW）计算结果与分析

与低双塑性墙方案一样，对低双刚性墙方案，计算了不同本构模型E—μ、E—B（μ≥0.1）、E—B（μ≥0.25）、E—B（μu=0.333）、DS—E—μ、EP—E—μ、EP—E—B（μ≥0.1），墙间水位变动（升、降），墙底端强风化变软，沉渣等因素对防渗墙位移和应力的影响。

6.4.1 基本方案各种本构模型的计算结果

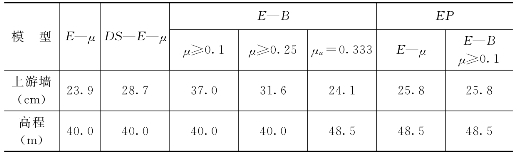
基本方案指上游水位85.0m，墙间水位40.0m，沉渣E=1×103MPa。

（1）墙体水平位移。各种本构模型计算的墙体水平位移如图6.4.1所示，各模型计算的墙体最大水平位移如表6.4.1所示。

表6.4.1 低双刚性墙方案各种本构模型计算的墙体最大水平位移

续表

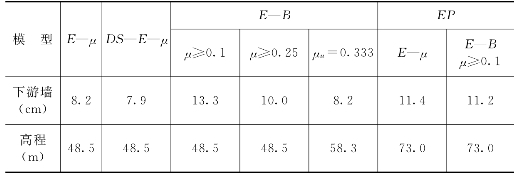
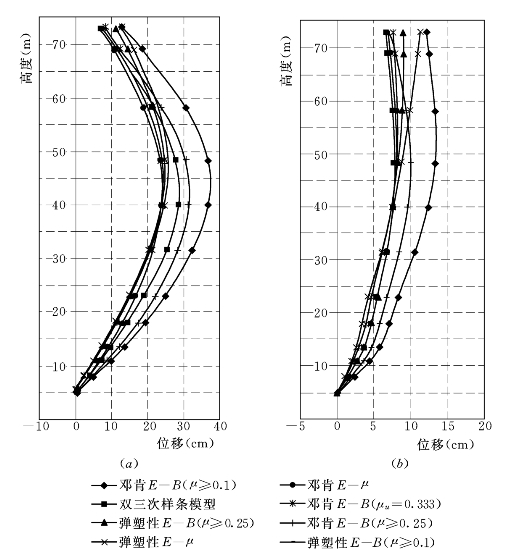
图6.4.1 低双刚性墙不同本构模型计算的墙体位移

（a）上游墙；（b）下游墙

各种模型中，上游墙最大位移为E—B（μ≥0.1）模型，最小为E—μ模型，下游墙最大也为E—B（μ≥0.1）模型，最小为DS-E-μ模型，除个别模型，上游墙的最大水平位移一般在25cm左右，下游墙的最大水平位移约8～10cm左右，水平位移比塑性墙方案普遍小，这是合理的，不同模型的位移规律同塑性墙方案的结果。

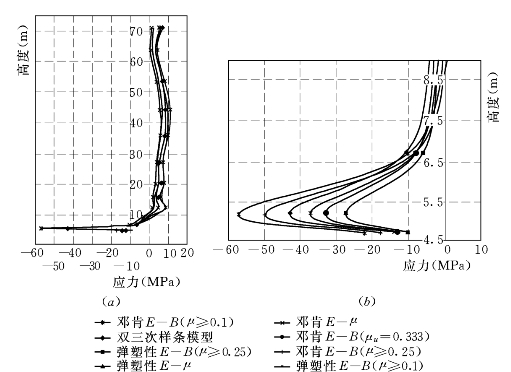
图6.4.2 低双刚性各模型计算的上游墙上游侧σy

（a）σy沿墙高分布；（b）墙底部σy放大图

（2）墙体的垂直应力σy。各模型计算的上、下游墙上、下游侧单元的σy如图6.4.3～图6.4.6所示，由图可见，各模型的σy的变化形状是类似的，最大拉压应力发生于墙底端岩面附近，该处应力最大为E—B（μ≥0.1）模型，最小的为EP—E—μ和EP—E—B（μ≥0.1）两个弹塑性模型，E—B（μu=0.333）模型次之。这主要是弹塑性模型在一定程度上可反映剪应力对体变的影响，说明弹塑性模型有一定的优点，结果与以上低双塑性墙方案的结果一致。

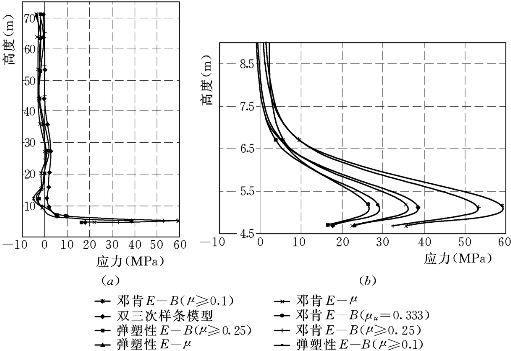
图6.4.3 低双刚性各模型计算的上游墙下游侧σy

（a）σy沿墙高分布；（b）墙底部σy放大图

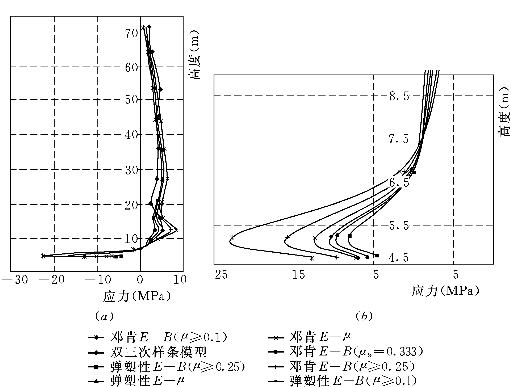
图6.4.4 低双刚性各模型计算的下游墙上游侧σy

（a）σy沿墙高分布；（b）墙底部σy放大图

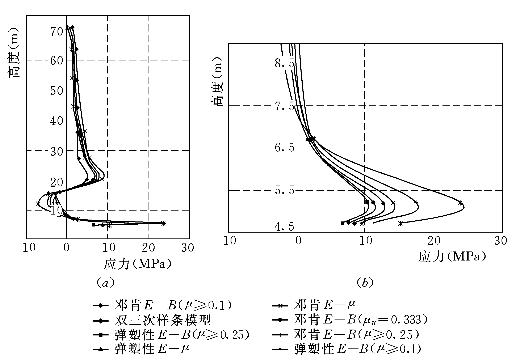
图6.4.5 低双刚性各模型计算的下游墙下游侧σy

（a）σy沿墙高分布；（b）墙底部σy放大图

（3）墙体单元破坏情况。以单元主应力判断墙体单元的破坏情况，当 为 压 应 力 时，σ1＞σc=150MPa，受 拉 时σ3＞σcτ=1.5MPa作为判别标准，表6.4.2给出不同本构模型墙底部破坏单元数。破坏单元以弹塑性模型最少，E—B（μ≥0.1）最多，且破坏单元数均远多于塑性墙方案，这一方面是由于塑性墙低弹模的作用，另一方面是其弹模非线性的作用。

不同模型墙体的破坏单元数统计如表6.4.2所示。

表6.4.2 不同本构模型墙体的破坏单元数（LDHW）

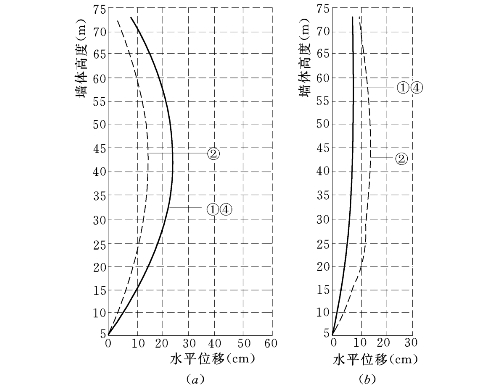
图6.4.6 低双刚性墙间水位变动对墙体位移的影响（E—μ模型）

（a）上游墙；（b）下游墙
①—基本方案；②—升水位至58.3m；④—降水位至31.6m

（4）堰体的沉降及水平位移。不同本构模型计算的堰体最大沉降及最大水平位移如表6.4.3所示。

表6.4.3 低双刚性墙方案不同本构模型计算的堰体最大沉降及水平位移（LDHW）(www.xing528.com)

由表可见，除E—B模型的值较大外，其他模型结果均较接近，最大沉降约50～60cm，最大水平位移约25～30cm。

6.4.2 墙间水位变动对墙体水平位移及墙体应力的影响

（1）墙体水平位移。不同模型墙间水位变动对墙体位移的影响规律都是一样的，即水位上升时，上游墙位移变小，下游墙位移变大，而水位下降时位移线与基本方案几乎重合，变化很微小，总的情况是水位上升对两墙的位移影响较大，水位下降的影响很微小。以E—μ模型和EP—E—μ模型为例，比较如图6.4.6、图6.4.7所示。

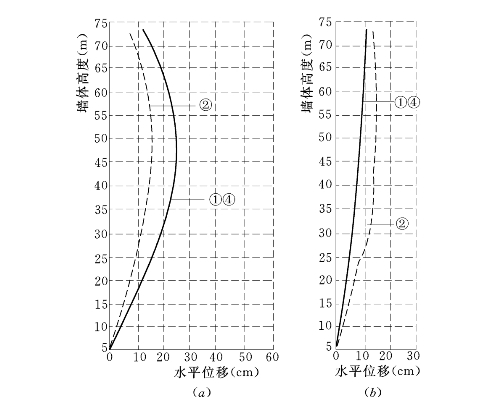
图6.4.7 低双刚性墙间水位变动对墙体位移的影响（EP—E—μ模型）

（a）上游墙；（b）下游墙
①—基本方案；②—升水位至58.3m；④—降水位至31.6m

（2）墙体垂直应力σy。墙体应力中的主应力和垂直应力σy的变化趋势是一样的。现以σy为例，比较由于墙间水位变动时σy的变化，以E—μ模型为例，比较如图6.4.8、图6.4.9所示，一般水位上升对上、下游墙的应力影响较大，水位下降影响很小，这一方面是下降的水位不大，另一方面下降水位时，两墙是相互加强的共同作用，而水位上升时则是两墙相互减弱的共同作用，故效果相差甚远。

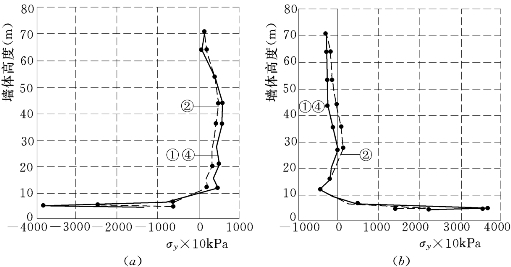
图6.4.8 低双刚性墙间水位变动对上游墙体σy的影响（E—μ模型）

（a）上游墙上游侧；（b）上游墙下游侧
①—基本方案；②—升水位至58.3m；④—降水位至31.6m负为拉应力 正为压应力

图6.4.9 低双刚性墙间水位变动对下游墙体σy的影响（E—μ模型）

（a）下游墙上游侧；（b）下游墙下游侧
①—基本方案；②—升水位至58.3m；④—降水位至31.6m负为拉应力 正为压应力

6.4.3 墙底沉渣对墙底应力的影响

设墙底（高程4.0～高程4.4）单元为沉渣单元，沉渣弹模设为E=1.0×102MPa，比基本方案中E=1×103MPa要低，墙底垂直应力σy及主应力在墙底端处均有降低。

6.4.4 墙底两侧强风化岩变软对墙底应力的影响

这里假定防渗墙的成槽施工破岩时，对墙体两侧一定范围内的强风化岩体有一定的影响，从而使墙体两侧的强风化岩在竖向有一排单元的弹模由原来的E=5×103MPa降为1×103MPa，该计算主要是研究这一变化对墙体底端应力的影响。

（1）墙体垂直应力σy的影响。各模型的计算结果表明，墙体底端的σy值都有所降低。

（2）墙体破坏单元数比较。各种模型计算结果表明，墙体破坏单元数有所减少，统计结果如表6.4.4所示，与基本方案的表6.4.2比较可见，上、下游墙的破坏单位数均有减少，说明强风化变软对刚性墙是有利的。

表6.4.4 墙底两侧强风化变软时墙体破坏单元数（LDHW—CR）

6.4.5 墙体混凝土采用各向异性本构模型对墙体应力的影响

该研究主要是考虑防渗墙混凝土单元出现超过混凝土的抗拉或抗压强度的应力时，材料在破坏主应力方向的弹模与另一主应力方向的弹模不等的情况，且破坏主应力方向的弹模取为一较小值E=1MPa，而另一方向的弹模则仍用原材料弹模，混凝土本构关系矩阵为各向异性的，考虑到墙体单元破坏主应力方向与墙体垂直方向较一致，故各向异性本构矩阵简化取为σx与σy方向的正交各向异性，由此而适当考虑墙体单元破坏或开裂对墙体刚度的影响，采用E—μ模型和EP—E—μ模型计算了低双刚性墙的基本方案。

（1）墙体垂直应力σy。以E—μ模型为例，考虑各向同性时上游墙的结果比较如图6.4.10所示，由此可见，考虑混凝土破坏后本构关系的各向异性后，σy最大应力降低较多。

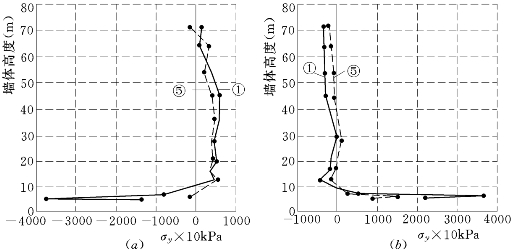
图6.4.10 墙体各向异性与基本方案的上游墙两侧σy比较（E—μ模型）

（a）上游侧；（b）下游侧
①—基本方案；⑤—墙体各向异性负为拉应力 正为压应力

（2）破坏单元。考虑混凝土各向异性后，E—μ及EP—E—μ模型的上、下游墙的破坏单元数统计如表6.4.5所示，与表6.4.2比较可见，墙体的破坏单元明显减少。

表6.4.5 低双刚性墙考虑混凝土各向异性时的破坏单元数

6.4.6 低双刚性墙方案小结

与塑性墙比较，低双刚性墙方案墙体水平位移小一些，而墙体破坏单元比塑性墙方案多，墙底端的应力状态以弹塑性模型最好。沉渣及强风化变软对墙体的应力影响较显著，这主要是墙体较刚之故。当墙体混凝土的本构关系考虑破坏后采用各向异性的本构模型时，墙体的应力有较大的改善，破坏单元减少较多，这种模拟更符合实际一些，但仍有破坏单元。