低双塑性墙方案的计算研究成果

6.3.1 基本方案各种本构模型的结果

基本方案指上游水位85.0m，两墙间水位40.0m的情况。

6.3.1.1 墙体水平位移

代表性的几种本构模型计算的上游墙及下游墙的水平位移如图6.3.1所示，各本构模型计算所得上、下游墙的最大水平位移及位置如表6.3.1所示。

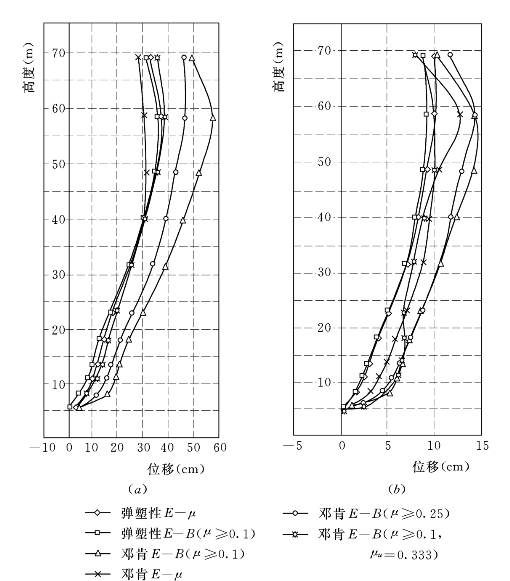
图6.3.1 不同本构模型计算的低双塑性墙墙体位移

（a）上游墙；（b）下游墙

表6.3.1 低双塑性墙基本方案防渗墙最大水平位移（LDPW）

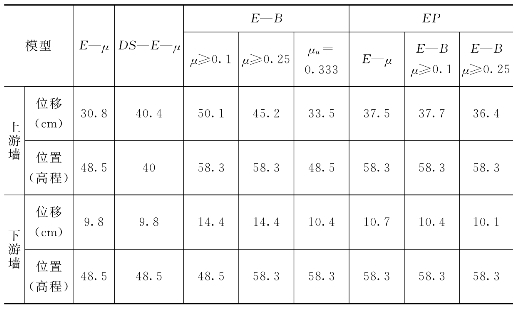
各模型中，最小位移为E—μ模型，上游墙30.8cm，下游墙9.8cm，最大位移为E—B模型中限定μ≥0.1的模型，上游墙50.1cm，下游墙14.4cm，几个弹塑性模型的位移值都相当接近，上游墙约为37cm，下游墙约为10cm，另外，E—B模型中限定卸载时μ=0.333的模型也与弹塑性的模型接近，从不同本构模型的位移情况，我们可得到的结果是：

E—μ模型与E—B模型比较：E-μ模型的位移小于E—B模型的位移，E—B模型中，限定μ≥0.1的模型的位移大于限定μ≥0.25的模型的位移，而限定卸载时μ=0.333的模型在E—B模型中位移最小，其与E—μ模型最接近，检查发现，E—μ模型的μ值普遍大于E—B模型中由E、B反算出的μ值，双三次样条函数E—μ模型的μ值也较小，因此，可以认为，μ值较小的模型，其墙体的侧向位移大，这从广义虎克定律中：

似乎也可以解释这一点，即在σx（水平力）作用下，在σy、σz变化差别不大时，则μ小，εx大，相应位移也大，从E—B模型中可见，限定μ≥0.25的模型的水平位移也小于限定μ≥0.1的模型，故E—B模型中也有一定的μ值是小于0.25的，而E—μ模型中，μ值一般大于0.25。

各种弹塑性模型中的水平位移较一致，主要是由于水压作用下，相对于原先以自重荷载为主的应力状态为卸荷状态，故此时弹塑性模型的μ值基本上为0.3，而E—B模型中限定卸载时μ=0.333的模型与弹塑性模型较接近，其原因也在于此。

因此，μ值对墙体的水平位移有较明显的影响。

6.3.1.2 墙体垂直应力σy

代表性的几种本构模型的上、下游墙的上游侧和下游侧的σy如图6.3.2～图6.3.7所示。比较关心的主要是墙底部岩面附近的应力，由图可见，各种模型的结果是有区别的，墙底附近最大σy值以弹塑性模型的值较小。

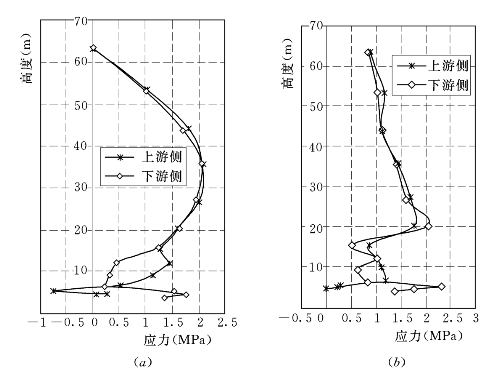
图6.3.2 邓肯E—μ模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

6.3.1.3 墙体的应力水平及主应力

基本方案中代表性的本构模型的上、下游墙各三排单元的应力水平如图6.3.8～图6.3.13所示，其左、右三排分别为上、下游墙的三排单元。

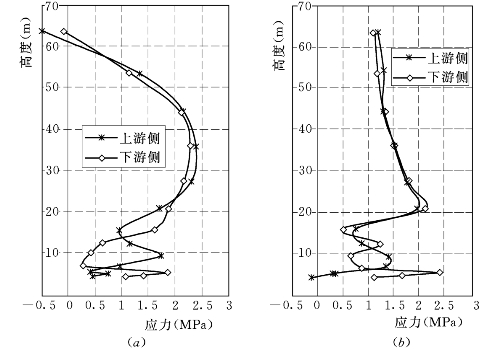
图6.3.3 邓肯E—B（μ≥0.1）模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

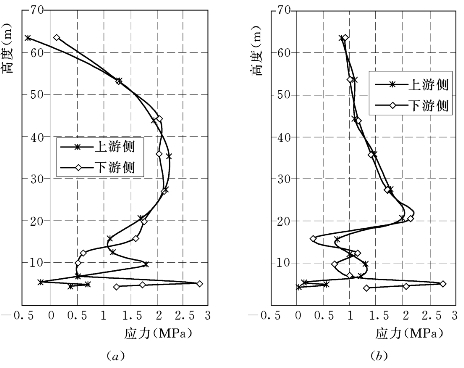
图6.3.4 邓肯E—B（μ≥0.25）模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

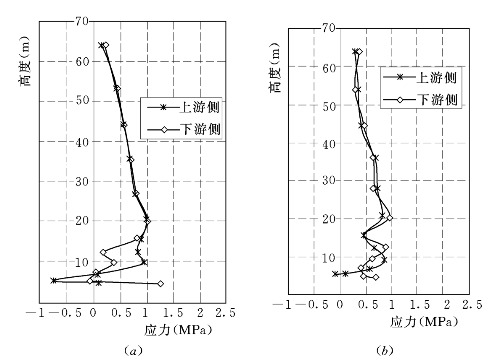
图6.3.5 邓肯E—B（μu=0.333）模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

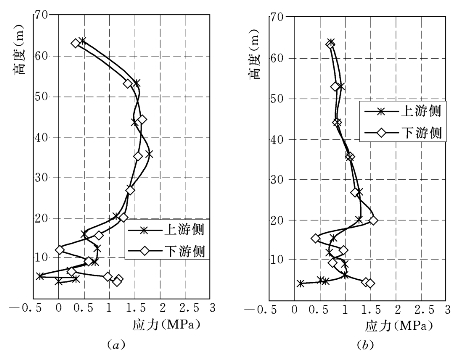
图6.3.6 弹塑性E—μ模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

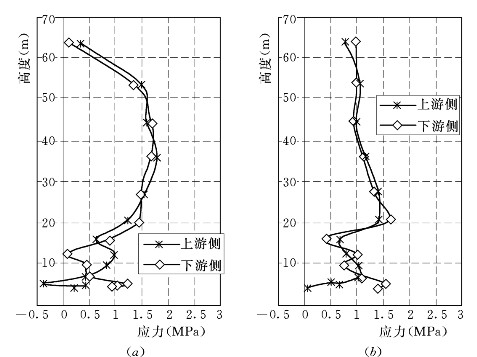
图6.3.7 弹塑性E—B（μ≥0.1）模型计算的墙体两侧σy值

（a）上游墙；（b）下游墙

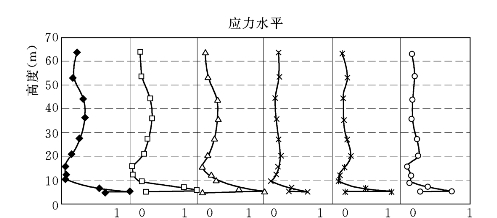
图6.3.8 E—μ模型计算的上、下游墙6排单元的应力水平

各种模型破坏的单元数主要集中在墙底岩面附近，统计如表6.3.2所示。

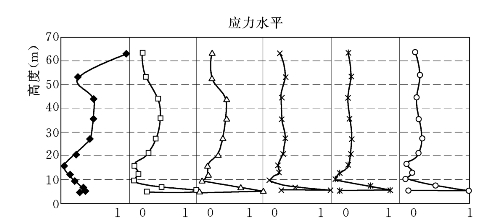
图6.3.9 E—B（μ≥0.1）模型计算的上、下游墙6排单元的应力水平

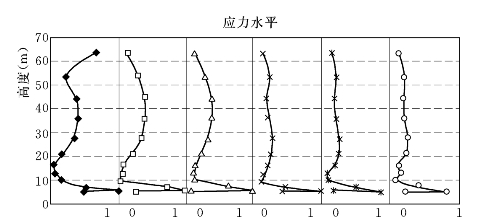
图6.3.10 E—B（μ≥0.25）模型计算的上、下游墙6排单元的应力水平

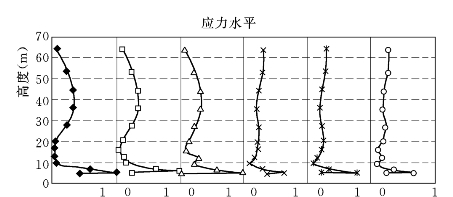
图6.3.11 E—B（μu=0.333）模型计算的上、下游墙6排单元的应力水平

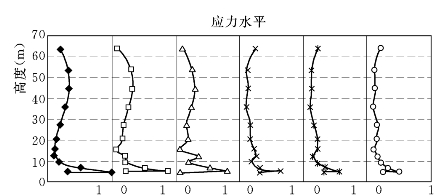
图6.3.12 EP—E—μ模型计算的上、下游墙6排单元的应力水平

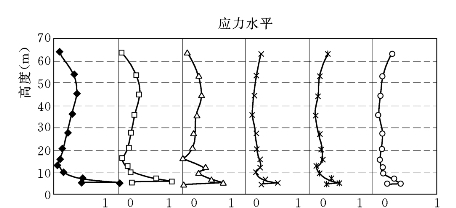
图6.3.13 EP—E—B（μ≥0.1）模型计算的上、下游墙6排单元的应力水平

表6.3.2 各种本构模型计算塑性墙体的破坏单元数（LDPW）

由以上的图和表可见，弹塑性模型的破坏单元数最少，在非线性模型中，以E—B模型中限定卸载时μ=0.333的模型和E—μ模型的破坏单元数较少。

6.3.1.4 堰体的沉降、水平位移及应力水平

各种本构模型计算的堰体最大沉降及水平位移如表6.3.3所示，E—μ、EP—E—μ模型堰体的沉降及水平位移如图6.3.14～图6.3.17所示。

表6.3.3 各种本构模型计算的堰体最大沉降及最大水平位移值

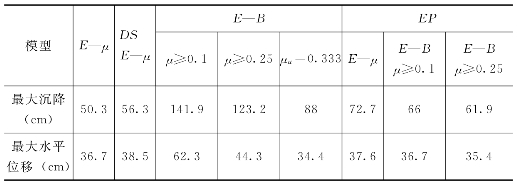
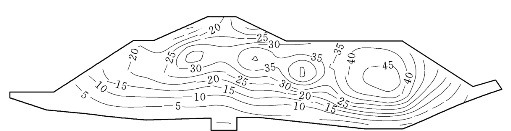
图6.3.14 E—μ模型计算的堰体沉降（单位：cm）

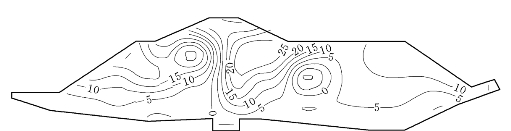
图6.3.15 E—μ模型计算的堰体水平位移（单位：cm）

最大水平位移基本上是在墙的下游侧，不同模型的位置接近，故数值相差也不大，除个别模型的位移偏大外，一般位移约在37cm左右，各模型计算的沉降值除E—B模型外，其他模型的最大沉降值一般在50～70cm附近。

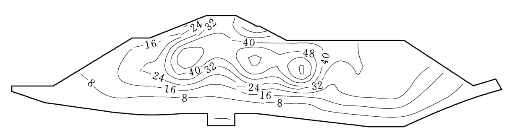
图6.3.16 EP—E—μ模型计算的堰体沉降（单位：cm）

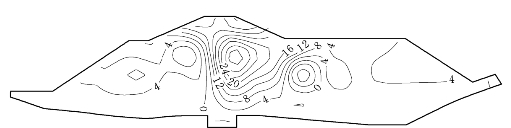
图6.3.17 EP—E—μ模型计算的堰体水平位移（单位：cm）

代表性模型E—μ、E—B（μ＞0.1）、EP—E—μ堰体的应力水平等值线如图6.3.18～图6.3.20所示，由图可见，各种模型在上游墙的上游侧有一较高应力水平的区域，这是由于墙体在水压力作用下产生水平位移，致使σ3值降低所致，E—μ模型在上、下游侧坡面中部也有稍高应力水平的区域，弹塑性模型则在子堤的迎水坡有较明显的高应力水平区域，弹塑性模型在堰体上、下游坡面附近的应力水平低于E—μ模型，E—B（μ≥0.1）模型破坏区较大。由堰体的应力水平表明，堰体除上游墙中部附近的上游侧有小局部破坏区（不影响堰体稳定）和子堤上游坡小局部有破坏区外，其余各处的应力水平均是安全的，因此，堰体是稳定的。

图6.3.18 E—μ模型计算的堰体应力水平

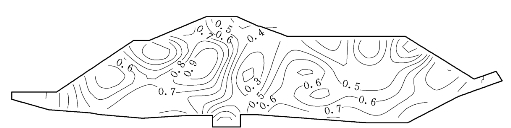
图6.3.19 E—B（μ≥0.1）模型计算的堰体应力水平(www.xing528.com)

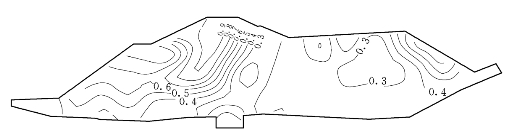
图6.3.20 EP—E—μ模型计算的堰体应力水平

6.3.1.5 不同本构模型计算结果的比较

（1）墙体水平位移。以E—μ模型最小，E—B模型较大，弹塑性模型居中，本构模型中μ值对墙体水平位移有较明显的影响，μ值小的模型，水平位移较大，μ值大的模型，位移小。

（2）墙体底部应力水平及破坏单元。墙体底部应力水平较高是以往较难解决的问题，本次计算中墙体破坏单元以弹塑性模型最少，E—μ模型及E—B（μu=0.333）次之，从破坏的单元来看，在墙底端部，上游墙有个别单元破坏，如弹塑性模型只有一个单元破坏；在墙的顶部，上游墙应力水平较高。下游墙弹塑性模型、E—μ模型及E—B（μu=0.333）都没有破坏单元，所以，塑性墙体应力在墙底部基本上不会成片破坏，故墙体应力基本是安全的。

（3）堰体的位移和应力水平。各种本构模型计算的堰体最大水平位移较接近，大部分模型约在37cm左右，不同模型的最大沉降值有明显的差别，几个E—B模型的沉降值最大，E—μ、DS—E—μ及EP模型较为接近，为50～70cm左右。

堰体的应力水平一般在上游墙的上侧及上、下游坡面的中下部高一些，破坏单元数很少，堰体是稳定的。

6.3.2 墙间水位上升方案（简记为LDPW—UW方案）

该方案主要是研究当运行期间两墙分担水头的不同对墙体应力的影响，当墙间水位上升至58.3m，上游水位为85.0m，即相当于下游墙承担2/3的水头，上游墙承担1/3水头的情况，同时，为分析水头变化对墙体位移和应力的影响，还计算了墙间水位由40.0m上升至48.5m时的情况，此节仅给出水位升至58.3m时的结果。由于本构模型的影响通过以上的分析已基本清楚，对该方案提供6个本构模型的计算结果，即E—μ、E—B（μ≥0.1）、E—B（μu=0.333）、EP—E—μ、EP—E—B（μ≥0.1）、DS—E—μ。

（1）墙体水平位移。墙间水位由40.0m上升至58.3m时，各种本构模型计算的上游墙和下游墙的水平位移如表6.3.4所示，与基本方案比较，上游墙的水平位移明显减小，下游墙水平位移则增大，这种趋势是合理的。

表6.3.4 墙间水位由40m上升至58.3m时墙体的最大水平位移及与高程40m 水位时的最大位移差值

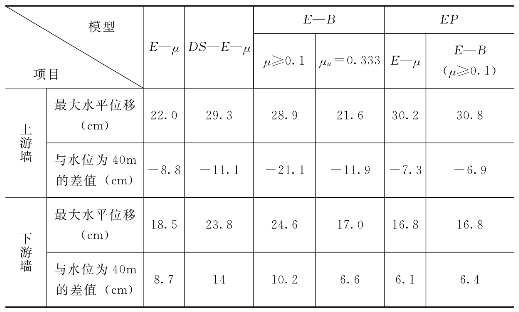
注 负值表示位移减少值，即向上游位移；正值表示增加值，向下游位移。

（2）墙体的应力水平。与基本方案比较，非线性模型在下游墙底端破坏单元数增加，弹塑性模型则没有增加，上游墙底端部应力水平有所降低，而下游墙的底端单元增加的应力水平幅度大于上游墙底端单元降低的幅度。墙间水位上升后，墙体破坏单元统计如表6.3.5所示。

表6.3.5 LDPW—UW方案墙体破坏单元统计数（水位升至58.3m）

6.3.3 墙间水位下降方案（简记为LDPW—DW方案）

该方案主要是研究当墙间水位由40.0m下降至31.6m时（相当于上游墙承担2/3水头，下游墙承担1/3水头），防渗墙的变形及应力情况。

（1）墙体的水平位移。各本构模型计算所得墙体的最大水平位移情况统计如表6.3.6所示。

表6.3.6 各种模型计算的塑性防渗墙最大水平位移（LDPW—DW）及与基本水位40m时的差值

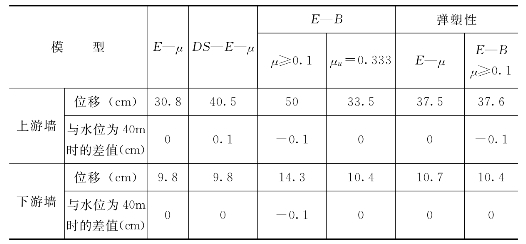
注 负表示减少值，即向上游位移；正表示增加值，向下游位移。

由上表可见，墙间水位下降后，上游墙的最大水平位移几乎没有什么变化，下游墙也没什么变化，这是由于一方面水位下降不大，另一方面，水位下降后对上游墙是加载，而对下游墙则是卸载，两墙的水平位移增量方向是相对着的，下游墙对上游墙提供支承作用，两墙共同作用分担其变化，因而对位移的影响较少。

（2）墙体的应力水平。墙间水位下降后，上游墙底端部的应力水平稍有所增大，下游墙应力水平稍有降低但影响甚微，上、下游墙的破坏单元数并未增加，故墙间水位下降对墙体应力的影响没有水位上升那样敏感。

6.3.4 墙间水位变动对墙体位移及应力水平的影响分析

（1）墙体水平位移的比较。水位上升对墙体位移影响较显著，而水位下降影响不大，这主要是水位上升时，上游墙卸载，下游墙加载，两墙的水平位移增量相背向，两墙不能相互加强，对下游墙影响较大，而水位下降时，上游墙加载，下游墙卸载，两墙的水平位移增量相向，下游墙向上游的位移抵抗了上游墙向下游墙方向的位移，两墙共同相互加强，故对上游墙的影响也不很大。

（2）墙体应力水平的比较。表6.3.7给出了不同水位状态时EP—E—μ模型、E—μ模型及E—B（μu=0.333）模型的下游墙墙底端的应力水平比较，单元位置如图6.3.21所示，由表可见，对下游墙底端，水位上升越高，其应力水平也高，水位降低时，单元应力水平也相应有所降低。但当水位升至58.3m时，E—B（μu=0.333）模型已有破坏单元出现，故以水位上升不宜超过50.0m为好。

表6.3.7 不同水位状态下下游墙墙底危险单元的应力水平（LDPW）

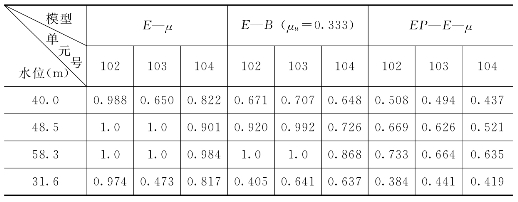
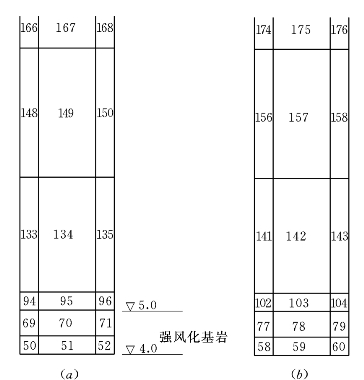
图6.3.21 防渗墙底部单元编号及位置

（a）上游墙；（b）下游墙

6.3.5 墙厚变化对墙体位移及应力水平的影响

本节研究塑性墙在基本方案中墙厚分别为0.8m、1.2m和1m时墙体位移和应力水平的情况，墙厚为0.8m时，墙体划分为3排单元，厚度分别为0.2m、0.4m、0.2m，墙厚为1.2m时，3排单元的厚度分别为0.3m、0.6m、0.3m，采用E—μ、E—B（μu=0.333）和EP—E—μ3个模型进行计算。

（1）不同墙厚墙体的水平位移。不同墙厚用不同的本构模型计算的墙体最大水平位移统计如表6.3.8所示。由表6.3.8可见，墙薄时，位移稍有增大，墙厚时，位移稍变小，这种变化是合理的，但变化不显著。

表6.3.8 不同墙厚各本构模型计算的墙体最大水平位移值单位：cm

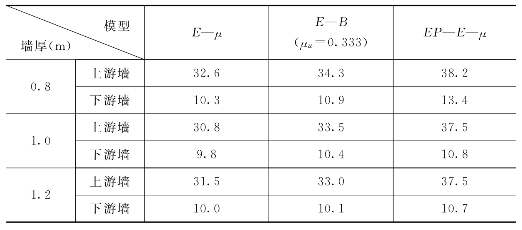
（2）墙体应力水平。在墙的底部最大应力水平区，以EP—E—μ模型为例，比较上、下游墙应力水平较大区域的几个单元如表6.3.9所示。

由表6.3.9可见，墙底端的最大应力水平区以墙厚为0.8m的应力水平最大，而墙厚为1.0m和1.2m的相差不多，因此，墙厚选择为1m是合适的。

表6.3.9 不同墙厚EP—E—μ模型墙体局部单元应力水平（LDPW）

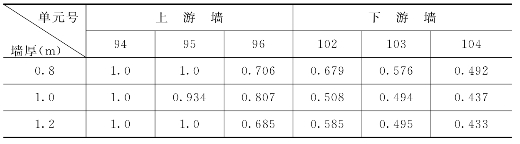
6.3.6 墙底两侧强风化岩变软对墙底应力的影响

这主要是考虑防渗墙施工成孔过程对墙体两侧强风化岩体的影响，使其弹模有所降低的因素，设定墙两侧强风化竖向一排单元的弹模由原来的E=5×103MPa变为E=1×103MPa，计算由此对墙体应力水平的影响，结果表明，其对应力水平的影响甚微。

6.3.7 墙体单元应力水平的可靠性分析

本节主要考虑水下40m高程以下风化砂E—μ模型参数K值变化对墙体应力水平的影响，目前所采用的K值为K=330，设风化砂参数的变化主要为K值的变化，取K的均值为-K=330，且假设K值的变化范围为：K值服从正态分布，且K值位于250≤K≤410的概率为90%，相当于K值小于410的概率为95%，即：

查正态分布概率表得[52]：

均值μ=330，则：

已知正态分布的均值μ和标准差σ或方差为σ2，则可以产生符合这一分布特征的随机数序列，本计算中，采用了100个满足以上分布条件的随机数Ki（i=1，100），对这100个Ki，用E—μ模型和EP—E—μ模型计算了墙体各单元的应力（σ1i，σ3i），由应力（σ1i，σ3i）（i=1，100）和莫尔—库仑破坏准则统计墙体各单元的失效概率。

对E—μ模型和EP—E—μ模型，表6.3.10给出了在以上条件下失效概率大于0的单元及其失效概率。

表6.3.10 失效概率大于零的单元及失效概率

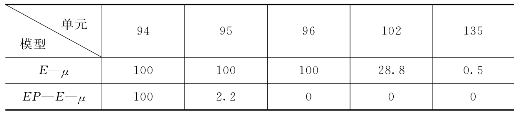
与K=330时的计算结果比较，则K=330时各模型判为破坏的单元，其失效概率为100%，不破坏的单元，其失效概率都不大，只有E—μ模型中下游墙102号单元，其原应力水平S=0.988已接近破坏状态，故此时的失效概率也只是28.8%，因此，可以认为，40m高程以下抛填风化砂参数变化时，对墙底端的应力水平影响不是很大，其原因主要是塑性墙材料为非线性材料，弹模低，具有较好的适应能力，故墙底端应力对40m高程以下抛填风化砂的敏感性不大。

6.3.8 低双塑性墙方案及不同本构模型的结果小结

通过以上的计算分析，对低双塑性墙方案采用不同本构模型得到如下的结果：

（1）墙体水平位移。以E—μ模型的结果最小，E—B（μ≥0.1）模型最大，其次为E—B（μ≥0.25）模型，EP模型及DS—E—μ模型、E—B（μu=0.333）模型居中，由此可认为，泊松比μ对墙体水平位移有较明显的影响，μ值小的模型计算出的墙体位移大，μ值大的模型计算出的位移小，但弹塑性模型受其影响则不大，原因主要是弹塑性模型卸载时μ取为定值0.3。

（2）墙体应力水平及破坏单元数。以EP模型[包括EP—E—μ、EP—E—B（μ≥0.1）、EP—E—B（μ≥0.25）]的破坏单元数最少，尤其是通常较为危险的墙底端，EP模型在上游墙有一个单元破坏，下游墙无破坏单元，其次为E—B（μu=0.333）模型，在上游墙有三个单元破坏，下游墙无破坏单元。下游墙在底端破坏的单元数较少，都在2个之内。

（3）堰体的位移及应力水平。以E—B模型计算的沉降较大，其他模型计算的沉降一般在50～70cm左右，各种模型计算的水平位移多数约在37cm左右。

堰体在上游墙的上游侧及子堤和上、下游坡面的中下部为高应力水平区，但破坏区很少，故堰体是稳定的。

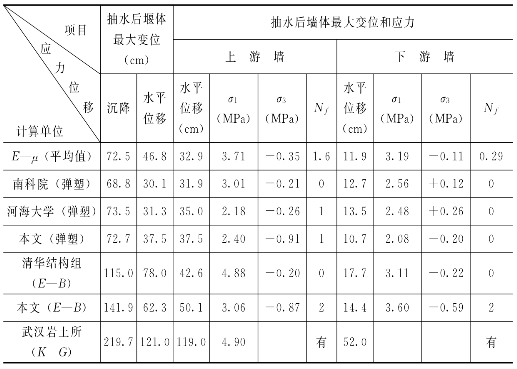
不同单位不同本构模型计算所得的墙体位移，最大应力及墙体破坏单元数据如表6.3.11所示[128]，由表可见，除E—B模型和K—G模型外，E—μ模型和各单位的弹塑性模型结果是相近的，弹塑性模型的破坏单元数少于E—μ模型，不同单位的弹塑性模型都表明了这一点，说明不同模型对计算结果是有影响的，因此，用不同模型进行比较计算是很有必要的。从本章不同E—B模型的研究可知，E—B模型一般μ值偏小，故对本工程，用E—μ模型或弹塑性模型计算较为合理。

表6.3.11 不同单位不同本构模型的计算结果

（4）墙间水位变化对墙体位移及应力的影响。墙间水位上升对下游墙的影响较为明显，会增大下游墙的水平位移和墙底端的应力水平，当水位由40.0m上升至58.3m时，相当于下游墙承担2/3水头，此时下游墙底端的应力除EP模型[包括EP—E—μ、EP—E—B）（μ≥0.1）、EP—E—B（μ≥0.25）]不产生破坏单元外，其他模型均有2～3个单元破坏，当水位上升至48.5m时，E—B（μu=0.333）模型有一个单元接近破坏。当墙间水位下降时，对墙体的位移及应力水平的影响都很小，这是由于此时两墙共同加强作用的结果。因此，墙间水位在▽40.0m左右是合适的，墙间水位上升时也不宜超过50.0m。

（5）墙厚变化对墙体的位移影响甚微，当墙厚为0.8m时，墙体应力水平（危险地段）明显提高，而墙厚为1.2m时与1.0m时的结果接近，因此，墙厚为1m是合适的。

（6）强风化岩弹模变化对墙体应力水平影响很小。

（7）根据可靠性分析表明，40m高程以下抛填风化砂参数变化对墙体高应力区的单元应力水平影响不大。

（8）对该方案的评价。以目前推荐的基本方案，两墙底端的应力状态基本上是安全的，再考虑一些有利因素（如河床的空间效应等），该方案是可行的。