6.2.1 本构模型
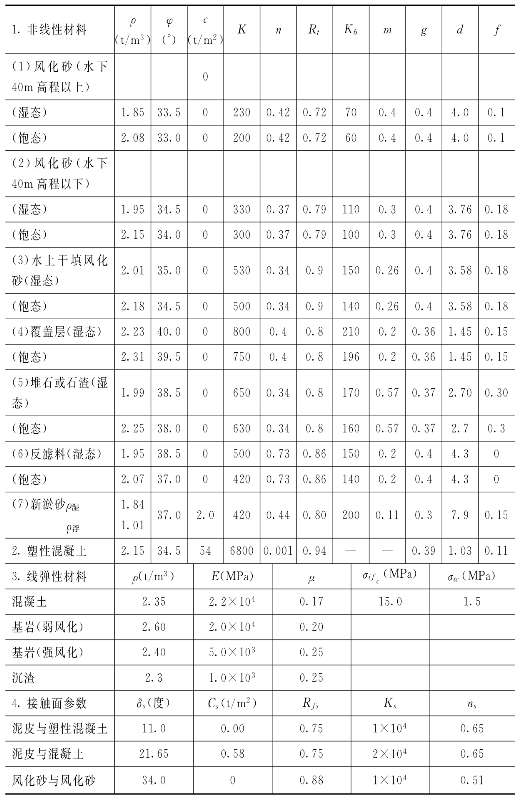
对堰体材料采用了不同的本构模型进行计算分析，本构模型的参数或试验曲线由长江科学研究院提供，如表6.2.1所示。
表6.2.1 三峡工程二期围堰计算参数表
本章所采用的模型有：邓肯—张E—μ模型、邓肯E—B模型，双三次样条函数E—μ模型以及应变空间弹塑性模型，对各种模型简介如下。
6.2.1.1 邓肯—张E—μ模型[5]（简记为E—μ模型）
6.2.1.2 邓肯E—B模型[126]（简记为E—B模型）
Et与式（6.2.1）相同
E、μ、B的关系为：
拟合结果如图6.2.1所示。
6.2.1.3 双三次样条函数E—μ模型[32]（简记为DS—E—μ模型）
该模型用双三次样条函数表示试验曲面：
当σ3=const.时，切线模量Et和泊松比μt由样条曲面求导而得，可由已知的m×n个型值点的（σ1-σ3）及边界条件通过插值得到：
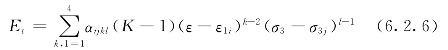
式中：ε1i≤ε≤ε1（i+1） σ3j≤σ3≤σ3（j+1）
（i=1，2，…，n-1，j=1，2，…，m-1）
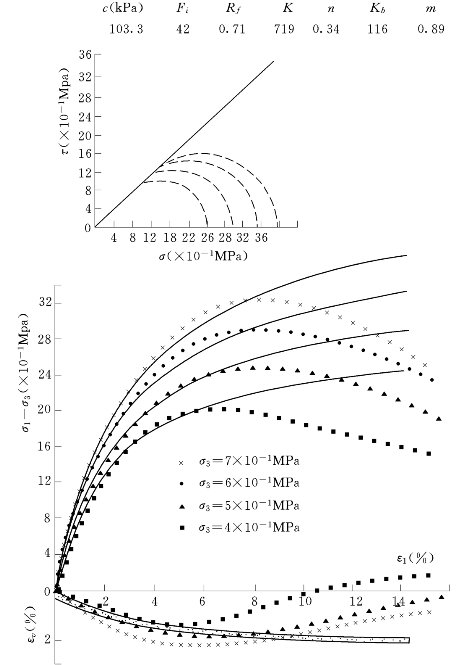
图6.2.1 石渣料（湿态）（ρd=1.97t/m3）三轴试验与E—B模型拟合曲线
式中：
（i=1，2，…，n-1，j=1，2，…，m-1）
对二期围堰的堰体材料，根据试验结果[127]，选择有代表性的试验曲线进行整理，由式（6.2.6）、式（6.2.7）求得Et、μt后，转换为应力空间（σ1，σ1-σ3）表示的结果：
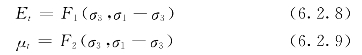
代表性的结果如图6.2.1、图6.2.2所示，其中图6.2.1为试验结果及曲线，图6.2.2（a）、图6.2.2（b）为双三次样条函数表示的空间试验曲面；图6.2.2（c）、图6.2.2（d）为求得的E、μ空间图，这样只要知道了单元的应力（σ1，σ1-σ3），就可由Et，μt的空间图形通过插值而求得其相应的Et、μt，有了Et、μt即可以像邓肯—张模型一样，由广义虎克定律建立应力应变矩阵。
对二期围堰，淤砂及砂卵石层没有试验曲线，我们采用了ρd=1.91t/m3的石渣料试验曲线代替淤砂，采用ρd=1.97t/m3的石渣料试验曲线代替砂卵石层。
6.2.1.4 应变空间弹塑性模型[122]（简记为EP模型）
弹塑性模型与以广义虎克定律为基础的非线性模型比较，其应力应变矩阵（弹塑性矩阵[Dep]）是满阵的。由多重势面理论[114]或张量定律[119]，可建立应变空间上的弹塑性应力应变关系为[122]：
弹塑性矩阵[Dep]为：
其中[De]为弹性矩阵，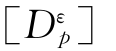
为应变空间表示的塑性矩阵。
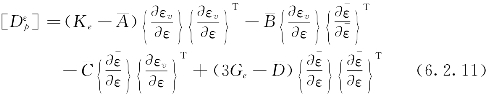
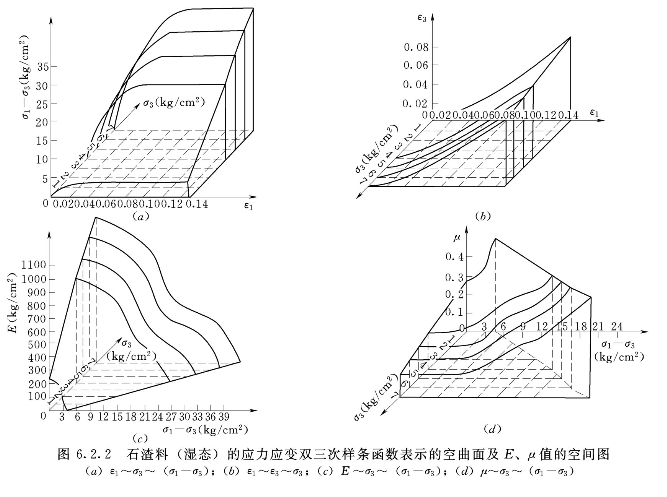
式中：Ke，Ge为弹性体积模量和剪切模量，取弹性时μ=0.3，弹性模量取为邓肯模型的Eur，Ke、Ge可由E、μ确定；
为广义剪应变；εv为体积应变，在常规三轴试验条件下（σ3=const.）；系数
可以用Et、μt来表示，有关公式见上一章。
Et、μt可由邓肯—张E—μ模型或E—B模型来确定。
6.2.2 加卸载准则
为比较不同模型的结果，加卸载准则统一用应力水平S来确定，设Sm为该单元历史上的最大应力水平，则
当S≥0.95Sm时，取Et′=Et
当S≤0.75Sm时，取Et′=Eur
其中：Eur为卸荷模量；Et′为计算采用的切线模量；Et为按模型计算的切线模量。
当0.75Sm＜S＜0.95Sm时，取：
其中：
6.2.3 接触面模型
接触面模型采用Goodman节理模型，切向刚度系数为：
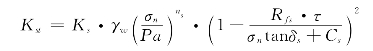
Ks、ns、Rfs、δs、Cs为计算参数，σn为法向应力。
当σn＜0时，令Kst=1.0t/m3
当接触面受压时，令Kn=108t/m3
当接触面受拉时，令Kn=1.0t/m3
6.2.4 计算的模型方案及补充规定
（1）邓肯—张E—μ模型（简记为E—μ模型）：当μ≥0.49时，取μ=0.49。
（2）E—B模型[简记为E—B（μ≥0.1）模型]：当μ≤0.1时，取μ=0.1；当μ≥0.49时，取μ=0.49。
（3）E—B模型[简记为E—B（μ≥0.25）模型]：当μ≤0.25时，取μ=0.25；当μ≥0.49时，取μ=0.49。
（4）E—B模型[简记为E—B（μu=0.333）模型]：当μ≤0.1时，取μ=0.1；当μ≥0.49时，取μ=0.49；当为卸荷（S＜Sm）时，取μ=0.333。
（5）弹塑性E—μ模型，（简记为EP—E—μ模型）：E，μ取法同①；卸荷为S＜Sm。
（6）弹塑性E—B模型[简记为EP—E—B（μ≥0.1）模型]：E、B取法同②；卸荷S＜Sm。
（7）弹塑性E—B模型[简记为EP—E—B（μ≥0.25）模型]：E、B取法同③；卸荷S＜Sm。
（8）双三次样条E—μ模型（简记为DS—E—μ模型）：卸荷时的弹模取Eur=E/（1-S1）2，E为样条插值得到的加载切线模量，S1见式（6.2.2）。(www.xing528.com)
在以上各模型方案中，E—μ、E—B模型求初始Ei时均用该单元历史上最大的σ3，样条函数模型插值也用该单元历史上最大的σ3值。
6.2.5 非线性计算方法
每级荷载均采用中点应力刚度法进行计算。
对第i级荷载增量{ΔPi}
由{σi+1/2}求得中点刚度矩阵[Ki+1/2]
则
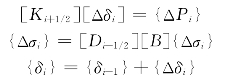
6.2.6 计算的防渗墙方案
目前设计推荐的方案为低双塑性墙方案，本章应用以上①～⑧种本构模型方案计算以下防渗墙的方案和情况：
6.2.6.1 低双塑性墙方案（简记为LDPW方案）
墙厚1m，入强风化岩1m，墙与墙的中心距离为6m，墙底端不设沉渣单元，墙体划分为三排单元，厚度分别为0.2m、0.6m、0.2m，两墙分担水头分4种情况。
有限元网格采用武汉水利电力大学提供的统一网格，如图6.2.3所示。
图6.2.3 低双墙方案有限元网格和材料分布
施工或加载次序为：初始应力场（冲淤砂以下单元）分2级，填筑过程分级为：
（1）抛填堆石体至高程69.0m，分5级加载。
（2）抛填过度（反滤）料至高程69.0m，分2级加载。
（3）抛填风化砂及右上角石渣至高程69.0m，分7级加载。
（4）抛填上游坡石渣至高程69.0m，分5级加载。
（5）水上碾压至高程73.0m，作1级加载。
（6）在高程73.0m平台建上游墙。
（7）碾压填筑子堤至高程83.5m，作1级加载。
（8）基坑抽水，由高程69.0m分2次降至40.0m，第一次降至58.3m，第二次降至40.0m，上游水位同时升至75.0m，作2级加载。
（9）在高程73.0m平台建下游墙。
（10）碾压填筑至坝顶高程88.5m，作1级加载。
（11）围堰进入运行期，两墙分担水头。
根据以上两墙分担水头的工况，水荷载分级见表6.2.2。
表6.2.2 两墙分担水头荷载分级
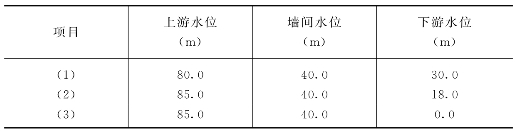
低双塑性墙方案除以上的基本方案外，还计算了墙间水位变化、墙厚变化以及墙体两侧强风化岩变软对墙体位移和应力的影响。
墙间水位的变化：
（1）墙间水位由40.0m上升至58.3m，相当于下游墙承担2/3水头，上游墙承担1/3水头。
（2）墙间水位由40.0m上升至48.5m。
（3）墙间水位由40.0m下降至31.6m，相当于上游墙承担2/3的水头，下游墙承担1/3的水头。
墙厚的变化：
（1）墙厚0.8m。
（2）墙厚1.2m。
墙体两侧强风化岩变软：考虑墙体两侧强风化岩一排单元由于冲孔时对岩体的影响，弹模由5×103MPa降为1×103MPa。
6.2.6.2 低双刚性墙方案（简记为LDHW方案）
计算条件及有限元网格同低双塑性墙方案，只是墙体材料改变，相应泥皮与混凝土的接触面参数也改变，同时考虑了墙底有沉渣，沉渣的弹模E分别为1.0×103MPa和1.0×102MPa的情况。
6.2.6.3 高双刚性墙方案（简记为HDHW方案）
有限元网格采用南京水利科学研究院提供的统一网格，如图6.2.4所示，施工或加载次序为：
图6.2.4 高双墙方案有限元网格和材料分布
（1）堆石至高程69m，分为8级荷载，每排单元作一级荷载。
（2）反滤带至高程69m，分为4级荷载。
（3）风化砂至高程69m，分为6级荷载。
（4）石渣至高程69m，分为4级荷载。
（5）水上干填至高程84.0m，作一级荷载。
（6）在高程84.0m施工下游墙。
（7）基坑限制性抽水至高程40m，墙上游水位82.3m，水荷载分二次施加，第一次为水荷载的1/3，第二次为水荷载的2/3。
（8）在高程84.0m施工上游墙。
（9）填至坝顶高程88.5m，墙顶高程85.0m。
（10）两墙分担水头时的水位：上游高程85.0m，墙间42.0m，水荷载分成1/3和2/3两次施加。
其他条件：
上、下游墙厚均取为1.2m，两墙中线间距离为6m，墙体单元为三排，厚度分别为30cm、60cm、30cm。
6.2.7 各计算方案及计算模型小结
计算方案如表6.2.3所示。采用的本构模型如表6.2.4所示。
表6.2.3 计算方案表
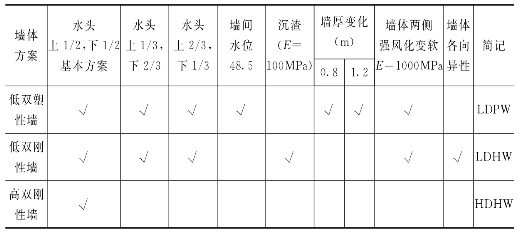
表6.2.4 计算的本构模型
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
