土体应变空间的多重势面数值弹塑性本构模型的应用

5.4.1 引言

通常的弹塑性模型是建立于应力空间的，且多是基于传统的塑性理论流动法则，模型参数的确定尤其不够方便，适应能力较差。在土的本构模型中，邓肯—张模型以其简单方便、参数确定容易且有明确的物理意义而得到最为广泛的应用，而其缺点则是不能反映土的剪胀性；二是采用双曲线函数拟合试验曲线有一定的局限性，一些试验曲线有可能不符合双曲线，例如对于具有剪胀特性的体变曲线以及对于软化的试验曲线不能拟合。目前的弹塑性模型虽然在反映土体变形特性方面较邓肯—张模型优越，但在参数确定方面则远远不如邓肯—张模型简便，因而，真正能得到广泛应用的弹塑性模型则较少，剑桥模型虽较简单一些，但在用于表述具有剪胀特性的砂土方面也有其局限性[73]。因此，如何建立一个既可以像邓肯—张模型那样方便地确定模型参数，而又能较好地反映土体变形特性的实用模型是很有意义的。

5.4.2 应变空间上的简化多重势面弹塑性模型

应变空间上表述的弹塑性模型具有较应力空间上更好的优越性[25，29]。上一节已根据多重势面理论提出了一个简便的应变空间弹塑性模型[121]，该模型的参数可以直接应用邓肯—张模型的两个参数Et、μt来表示，其本构方程为：

式中：为应变空间表示的弹塑性矩阵：

[De]为弹性矩阵，为应变空间表示的塑性矩阵：

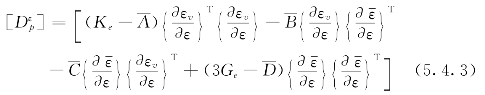
Ke、Ge分别为弹性体积模量和弹性剪切模量，系数由上节可知，在假定材料服从关联流动条件下可由Ke、Ge、Et和μt来表示。Et、μt的定义同Duncan—Chang模型，即：

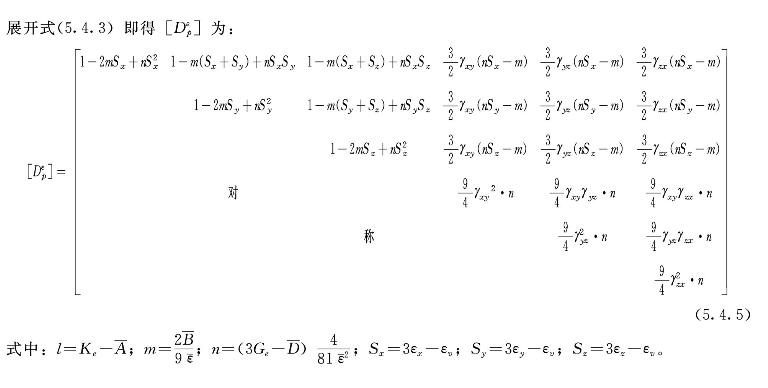
轴对称条件下，{dσ}=[dσr，dσθ，dσz，dτγθ]T，{dε}=[dεr，dεθ，dεz，dγγθ]T，以（γ，θ，z）坐标系对应（x，y，z）坐标系而得，此时[]应为式（5.4.5）中保留第1，2，3，6的行和列交叉的元素。

这样，只要知道材料的弹性参数E、μ和弹塑性状态时由式（5.4.4）定义而确定的Et、μt，即可由以上的结果而得到可用于有限元分析的增量本构方程。上一节中采用了邓肯—张模型的方法确定Et、μt而用于有限元计算，但由于一些土体具有剪胀性时，其εv～εa曲线用双曲线表达时误差较大，其μt＞0.5时不能反映。再者，双曲线方程对一些土体的适应范围仍是有限的。对εv～εa的拟合，程展林[59]则采用坐标旋转的方法来应用双曲线函数拟合，但若用邓肯—张模型则始终无法反映剪胀阶段的结果。因此，本文应用以上的弹塑性模型，但采用数值方法来求Et、μt，这样可使其适应性更广。

5.4.3 试验曲线的拟合及Et、μt的数值表示

由以上的分析可见，在假定材料服从关联流动的数学条件后，弹塑性本构方程关键是Et、μt的确定，这可以由常规的三轴试验σ3=const.的试验结果而得到，一般试验所得到的关系为不同σ3值时q～εa、εv～ε1的关系，其示意图如图5.4.1所示，当σ3=const.时

则

故

因此，只要知道q～ε1、εv～ε1方程，则任一状态时刻的Et、μt即可以 由 式（5.4.6）、式（5.4.7）而求得。由图5.4.1可见，一般情况下，对某一试验的σ3，可用函数拟合，如多项式最小二乘拟合法来拟合试验点而得到拟合函数：

图5.4.1 剪胀性土的应力应变试验曲线

则由式（5.4.8）和式（5.4.6）、式（5.4.7）的定义可得：

因试验的σ3值是有限的，由式（5.4.9）可得到某些（ε1，σ3）点对应的型值点Et、μt，可组成如表5.4.1和表5.4.2的数据表。

表5.4.1 Et 与应力和应变的关系表

表5.4.2 μt 与应力和应变的关系表

有了这样的表格，则对表格最大范围内的任一点应力应变状态（σ3，ε1），可采用二元三次插值多项式，由其相邻的9点（σ3i，ε1j）插值而求得，为方便，令x=σ3，y=ε1，则 插 值 公式为[123]：

Etrs为相应于型值点（xr，ys）处的函数值，同理可对μt进行插值。相应这种插值公式已有现成的程序可用[123]。对于形成表5.4.1、表5.4.2可用多项式最小二乘法拟合各σ3i下的试验曲线，现有的一些应用软件中都配备了各种曲线拟合的功能，因此，其拟合工作是很方便的，拟合得到曲线方程后，即可由式（5.4.9）求导而得到每条试验曲线中任意点（σ3i，ε1j）上的Et、μt值，从而得到表5.4.1、表5.4.2。

Et、μt也可以转换成（σ1-σ3，σ3）之间的关系，此时的型值点为[σ3i，（σ1-σ3）j]，可按（σ1-σ3）与ε1的关系曲线，如图5.4.2所示，根据某一σ3试验条件下的（σ1-σ3）插值出其对应的ε1，即得到（σ3，σ1-σ3）与（σ3，ε1）为对应点，再由（σ3，ε1）从式（5.4.6）、式（5.4.7）求得其相应的Et、μt值，则该值即为对应于（σ3，（σ1-σ3））点相应的Et、μt型值。采用这种形式的数值型值点表格如表5.4.3、表5.4.4所示，这种应力空间表示的型值点对于软化材料时会出现多值情况，如图5.4.2所示，因同一（σ1-σ3）值与曲线的交点有两个点，一个为交于硬化阶段，一个为交于软化阶段，故此时还必须要给定软化的判别式，而应变空间表示则何时都是单值函数，其相对要较为方便一些。

图5.4.2 软化及剪胀性土的q～ε1～εv关系图

表5.4.3 Et 与应力和应变的关系表

由此可得到不同应力状态或应力应变状态下用数值表示的Et、μt一组数据，形式如表5.4.1、表5.4.2或表5.4.3、表5.4.4所示，对不同应力状态（σ3，（σ1-σ3））或应力应变状态（σ3，ε1），根据以上表格可由式（5.4.10）插值求得其相应的Et、μt值，再加上弹性状态时的E、μ，即可由以上方法得到分析所需的弹塑性本构方程。

表5.4.4 μt 与应力和应变关系表

5.4.4 试验及模型的应用

为检验模型的性能及其反映土体剪胀特性的能力，对一碎石桩复合土体的三轴试验应用邓肯—张模型和以上的数值弹塑性模型进行有限元计算，并分析其共同作用的机理。

5.4.4.1 研究方案

碎石桩复合土体试样如图5.4.3所示，试样直径为φ101mm，高为200mm圆柱试样，其中心直径为φ39mm的碎石桩。试样在三轴仪上进行剪切试验，在试验中力图保持轴向为平面变形，采用特制的应力帽，可以分别得到碎石及土体部分上各自分担的应力，然后分别对碎石和素土单独进行三轴试验，测定其应力应变关系曲线，建立相应的邓肯—张本构模型和本文的数值弹塑性本构模型，应用所建立的模型对复合试样进行有限元计算分析，将计算结果与复合试样试验结果进行比较，主要是考察碎石和其周围土体各自分担的应力和应变关系。由于碎石和土体是两种性质不同的材料，两者在轴向变形协调条件下分担的应力必是不同的，这是两种材料的共同作用问题，而碎石体是一种剪胀材料，可以用于检验本构模型在反应剪胀特性方面的能力和剪胀对于共同作用的机理的影响。

图5.4.3 复合体试样

A1—碎石桩；A2—素土；D1=39mm；D2=101mm

5.4.4.2 碎石和素土的本构模型

碎石和素土的物理指标如表5.4.5和表5.4.6所示[124]。素土的含水量和容重同复合试样中的土体，碎石也控制与碎石桩具有相同的密度。碎石的三轴试样直径39mm，高为80mm，ρd=1.70g/cm2，相对密度Dr=75%，不同围压下主应力差σ1-σ3与轴向应变ε1和体应变εv的关系曲线及采用GRAF软件中的多项式拟合函数拟合的结果如图5.4.4和图5.4.5所示。其优点在于比以往用经验数学函数模型拟合都好。

表5.4.5 碎石物理力学性质

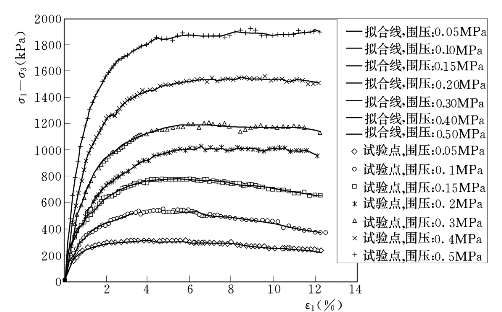
图5.4.4 碎石三轴试验的应力应变曲线及数学拟合结果

图5.4.5 碎石三轴试验的εv～ε1关系曲线及数学拟合结果

表5.4.6 素土料物理力学性质

(www.xing528.com)

对拟合所得的函数进行求导求得各曲线不同点的Et、μt值，Et、μt与（σ3，ε1）关系如图5.4.6、图5.4.7所示，实际应用时，图5.4.6、图5.4.7的关系为一组数据。由图5.4.7可见，当材料发生剪胀时，则μt＞0.5，这种特性是以广义虎克定律为基础的模型较难反映的。

图5.4.6 碎石Et～（σ3，ε1）空间图

图5.4.7 碎石μt～（σ3，ε1）空间图

碎石的邓肯—张E—B模型数据采用文献[124]的结果，如表5.4.7所示。

表5.4.7 碎石的E—B模型材料参数

素土采用白河堡黏土，素土三轴试验试样直径101mm，高为200mm，干密度ρd=1.55g/cm2，试验控制在ρd=（1.55±0.01）g/cm2之间，具体试验结果可参考文献[124，125]，试验所得的σ1-σ3～ε1关系及函数拟合的结果如图5.4.8所示，εv～ε1的关系及函数拟合结果如图5.4.9所示，求导后所得到的Et～（σ3，ε1）关系如图5.4.10所示，μt～（σ3，ε1）关系如图5.4.11所示，实际本构关系输入的是μt～（σ3，ε1）关系的数据型值点。同理用邓肯—张模型整理所得的素土E—μ模型参数如表5.4.8所示[124]。

表5.4.8 土体的E—μ模型材料参数

图5.4.8 素土的三轴试验应力应变关系曲线及数学拟合结果

图5.4.9 素土三轴试验的εv～ε1关系曲线及数学拟合结果

图5.4.10 素土Et～（σ3，ε1）空间图

5.4.4.3 复合体的试验结果和计算结果的比较

完成的复合体试验分两部分，第一部分为复合体的三轴试验，第二部分为纯土的空心圆柱加内压的三轴试验，第一部分共完成了σ3=50kPa、σ3=100kPa和σ3=150kPa的试验。本文主要研究围压σ3=100kPa的情况，为尽量模拟竖直方向平面应变条件，采用了图5.4.12所示的加载板，加载板受力后通过调压阀来调节测压管中的油水液面，使其保持不变，以此来保证底板处于同一平面，三轴试验系统布置示意图如图5.4.13所示。图5.4.12（a）为通过水压调节测出土面的应力，而碎石桩所受荷载则由总荷载N减去土体承担的荷载而得到，由此可分别得到碎石桩和周围土体的应力，这部分的试验结果见文献[124]。图5.4.12（b）则是通过水压调节测出碎石桩面上的应力，土体应力由总荷载减去碎石桩承担的荷载除以土体截面积而得到，试验发现两种试验的结果其碎石桩的应力有一定的差别，图5.4.12（a）方法测得的碎石桩应力高于按图5.4.12（b）方法测得的应力，实际的碎石桩应力和土体应力则采用了两种方法所得结果的应力平均值作为试验值与计算结果进行比较分析。第二部分的试验主要是用于检验有限元计算的可靠性。计算采用轴对称有限元，有限元网格及计算边界条件如图5.4.14所示，在刚性板底部与土体及碎石接触的部位设有Goodman节理单元，节理单元参数取值较小，以减少接触面对试样的侧限，取为Ks=10MPa，ns=0.5，Rf=0.7，c=1kPa，φ=4°，设定刚性板上各节点的位移相同，这样可保证在竖直方向的平面变形，数值模型中的弹性参数E取为初始模量，统一取为ε1=0.5%时的切线模型量，取μ=0.3，试样的垂直平均应变为更好与试验一致，采用总位移与试样长度之比作为试样的平均应变，加载时，先在侧面和顶面加σ3=σ1=100kPa作为围压，逐级加载则在轴心处刚性板上用集中力N进行模拟实际加载。复合试样试验和两种模型计算所得的土体（σ1-σ3）～ε1关系如图5.4.15所示，图中也附上了纯土体在σ3=100kPa时的（σ1-σ3）～ε1关系曲线，图中还给出了数值弹塑性模型中弹性参数Eur按邓肯—张模型方法确定时的结果，由图可见，其与用初始段的切线模量的结果是相近的，试验与计算结果较接近，弹塑性模型在后期略高于试验值，而邓肯—张模型则低于试验值，较接近于素土的结果，但略为高于素土，这是由于复合体中有硬于素土的碎石体，故邓肯—张模型略高于素土正是反映了碎石体的作用，由于邓肯—张模型不能反映碎石的剪胀特性，所以不能反映两者的相互作用。且碎石所占总截面积仅约15%，比例较少，故邓肯—张模型接近于素土而又略高于素土但低于复合体试验曲线的结果是合理的，弹塑性模型可以反映碎石的剪胀特性，其结果高于邓肯—张模型结果是合理的，说明反映了剪胀特性，从μt的数据上反映有μt＞0.5的情况，图中也说明数值弹塑性模型的结果较好一些。

图5.4.11 素土μt（σ3，ε1）空间图

图5.4.12 加载板剖面图

（a）方案一；（b）方案二

图5.4.13 复合体三轴试验系统布置示意图

图5.4.14 复合试样有限元计算网格图

图5.4.15 复合体三轴应力应变试验与各模型有限元计算结果的比较（σ3=0.1MPa）

图5.4.16为复合体中桩、土应力应变关系的试验结果与有限元计算结果的比较，图中也给出了σ3=100kPa时纯碎石和素土的应力应变关系进行比较，由图可见，素土的应力应变曲线高于复合体中土的应力应变曲线，而复合体中碎石的应力应变曲线高于纯碎石的应力应变曲线。其原因是由于复合体是两种力学特性不同的材料和共同作用的结果，因碎石具有剪胀特性，在剪切过程中会发生较大的体变而产生一个向外扩张的力，而其外周是土体，必然会对其产生一个箍紧的力，其共同作用的结果使得碎石桩的围压增加，而土体在碎石桩张力作用下其切向正应力σθ降低，如图5.4.17所示，这样，土体外周是σω=100kPa的水压力，而在碎石桩张力σi作用下，土体中σθ＜σω，故土体部分实际的σ3＜100kPa，土体的应力应变曲线则必低于素土在σ3=σω=100kPa下相应的应力应变曲线，而碎石桩由于受到外周土体的约束作用，σ3=σi＞σω=100kPa，故其相应的应力应变曲线必定高于实际纯碎石体在σ3=100kPa下的应力应变曲线，这一共同作用的机理由有限元计算所得的单元应力分布可反映出来。图5.4.18所示为碎石桩σ3～ε1的关系曲线的计算结果，由图可见，邓肯—张模型计算的σ3略有增加，而数值弹塑性模型的σ3则增大较多，说明碎石桩的σ3已远大于原初始值σ3=σω，因而碎石桩的（σ1-σ3）～ε1曲线高于σ3=100kPa时相应的曲线是合理的，而从图5.4.18可见，能反映碎石剪胀特性的弹塑性模型计算的碎石桩的σ3要高于不能反映剪胀特性的邓肯—张模型的结果也是合理的。

图5.4.16 复合体中桩、土应力应变与各模型有限元计算结果的比较

图5.4.17 碎石桩和周围土体共同作用示意图

图5.4.18 复合体中的碎石桩各模型有限元计算的最小应力σ3～ε1关系

图5.4.19、图5.4.20分别是两种模型有限元计算所得到的土体内圈与外圈单元σ3～ε1的关系曲线，由图可见，土体单元的σ3是逐步减少的，因而图5.4.16中复合土体中土体的（σ1-σ3）～ε1的关系曲线必低于纯土σ3=100kPa时相应的试验曲线，关键原因在于相互作用过程中最小主应力σ3已发生了变化，这是合理的。同时，弹塑性模型计算的土体σ3值低于邓肯—张模型的计算结果，而弹塑性模型计算的碎石桩的σ3则大于邓肯—张模型的结果，这主要是弹塑性模型比邓肯—张模型能更好地反映碎石的剪胀特性的结果，剪胀产生体变而形成较大的外张力，即碎石桩的σ3，碎石较大的外张力必使其周围土体的σθ=σ3变小，这在理论上是合理的。

图5.4.19 复合体中各模型有限元计算的土体内圈单元σ3～ε1关系

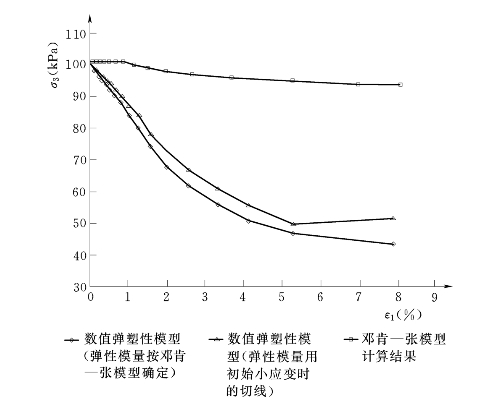
图5.4.20 复合体中各模型有限元计算的土体外圈单元σ3～ε1关系

通过以上模型计算所得的σ3的变化规律，再分析图5.4.16中的试验及计算的结果则较为容易理解其内存的机理了。由图5.4.16可见，碎石桩体试验的（σ1-σ3）～ε1曲线高于纯碎石体σ3=100kPa时的结果，是由于在复合体中由于碎石的剪胀作用和外周土体的箍紧作用，使碎石桩的σ3得以提高的原因，而外周土体的（σ1-σ3）～ε1低于素土在σ3=100kPa时的试验曲线则是由于碎石桩的剪胀产生的扩张力使土体的最小主应力σ3低于100kPa所致。而模型计算中，数值弹塑性模型中的碎石桩（σ1-σ3）～ε1计算曲线高于邓肯—张模型计算的曲线，主要是弹塑性模型能比邓肯—张模型更好地反映了碎石的剪胀特性，从而使弹塑性模型计算的碎石桩单元最小应力σ3高于邓肯—张模型计算的σ3的结果所致，如图5.4.18所示，因而其结果更接近实验结果，而土体单元中则差别较小一些，主要是所采用的土质对围压的敏感性不如碎石的敏感性，这可以从纯碎石和素土的三轴试验曲线上得到验证，碎石桩中σ3由100kPa增加至190kPa时，纯碎石的（σ1-σ3）～ε1曲线变化较大，而复合体中土体单元的σ3由100kPa减至50kPa时，素土的应力应变曲线的变化不如纯碎石的大。

为检验计算结果的可靠性，还利用素土做了一个空心圆柱的试验，内壁用橡皮膜加内压模拟弹塑性模型计算所得的碎石桩径向压力与轴向应变σri～ε1的关系，试样加压如图5.4.21所示，以此来测定空心素土圆柱的应力应变关系（σ1-σ3）～ε1，然后，由原复合试样的总轴向力减去素土空心圆柱承担的荷载，以计算获得碎石桩的应力应变关系。设某一应变ε1下复合体的截面平均应力为-σ，总截面积为A，碎石桩截面积为A1，土体部分的截面积为A2，已知土体部分的竖向应力为σ2，设碎石桩竖直向应力为σ1，则有关系：

由此可得到σ1为：

图5.4.21 模拟弹塑性模型计算的内压力σri的试验方法

由于A=A1+A2，故上式又可写成：

试验和分解后分别得到土体部分和碎石桩的应力应变曲线（σ1-σ3）～ε1如图5.4.16所示。由图可见，土体的试验曲线与计算曲线还是非常接近的，且明显低于素土的应力应变曲线，说明以上复合体试样共同作用机理的分析是合理的。分解所得到的碎石桩的应力应变曲线在与各种情况下的曲线比较中，其与弹塑性模型的计算曲线最接近，且趋向较一致，说明弹塑性模型计算结果是可靠的。但在初始段有一定误差，这种差别是存在的，因本身也是一种模拟和近似，况且土体截面在复合体中所占面积较大，达到75%，土体部分稍有误差都会对碎石桩的应力有较大的影响，因测量的是土体应力和总荷载，碎石桩应力是由总荷载减去土体承担的部分后分解出来得到的。

5.4.4.4 讨论

由图5.4.16的结果可见，复合体试验虽然采用了两种方案的平均值，以便减少试验与计算条件的差别，但试验值与计算值仍有一定的差距，这些差距的存在，一方面是计算所用的理想条件与试验的条件仍有差距，如垂直向平面变形的假设与试验变形的差距。再者，在本构模型的模拟方面，也很难说是十全十美，如对Et的确定，其定义的是沿ε1方向的方向切线斜率，实际上的应力路径是随ε1变化的同时，σ3也是变化的，如对于碎石桩，ε1增加时，σ3也是增加的，这是一硬化的过程。而对于周围的土体，在ε1增加的同时，σ3是减少的，即相当于土体部分是存在减压软化的，如图5.4.22所示的空间曲面。这样，对于围压增加的情况，按沿ε1的方向斜率定出的Et则是偏小的，反之，当减压情况时，则按目前的方法定出的Et则是偏大的。由此，当用于有限元分析其共同作用时，对碎石桩的刚度则可能是低于实际的，而对土体来说，则其刚度可能是偏高的，这样计算的结果则可能是碎石桩应力是偏低的，而土体是偏高的，实际结果也说明是这样的。但土体由于面积占绝大部分，而碎石桩截面积相对则较小，故对于碎石桩是比较敏感的，因而碎石桩的差别也较明显一些。另外，弹塑性模型为了简化也是作了假设的，如对A、B、C、D4个系数的关系，假定了是满足关联流动条件的，邓肯—张模型同样也是有假设的，因此，差别是肯定存在的。目前的计算结果与试验比较，计算结果基本合理和反映了共同作用的机理，尤其弹塑性模型，由桩体和土体σ3的变化规律可看出，该模型能较好地反映剪胀材料的共同作用的机理，但要得到更理想的结果，还需要做进一步精细的工作。

图5.4.22 Et随σ3变化的空间示意图

5.4.5 小结

本节依据广义位势理论中的多重势面理论基础上建立的应变空间数值弹塑性模型具有参数确定简便的优点，无需传统的塑性位势理论那样存在推求塑性势函数的复杂工作。而参数可通过拟合试验曲线而得到，且用数值方法表示时，其物理意义明确，直观，方便，比通常用经验数学函数表示的方法具有更广的适应性，可以利用现有的计算机软件中的函数拟合功能更为方便地求得用数据表示的参数。所建立的这一模型既保存了邓肯—张模型那样的简单性，而又具有更广的适应性，还可以反映土体的剪胀性，因此，是一个较有实用价值的模型。通过碎石桩复合体的试验和有限元计算结果表明，模型具有较好的反映土体剪胀特性的功能，计算结果较邓肯—张模型更接近试验结果。