简化多重势面弹塑性模型在土本构模型中的应用

5.2.1 简化多重势面弹塑性模型的本构方程

不考虑π平面上的影响，从常规三轴试验中可以得到～（p，q）空间上的增量关系

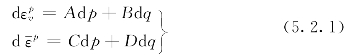
A、B、C、D为系数，文献[10]称其为塑性系数，p，q，dp，的定义同文献[41、67]，如下式所示

增量形式的塑性应变和应力增量，或dpp、dqp可以用增量的分量、代入εv、、p、q相应的公式中而得到。由以上的多重势面理论有[114]：

φk（k=1，2，3）为其梯度矢量线性无关的3个数学势函数，当仅在（p，q）空间上时，可看作为一个二维问题，则k=1，2，最为简单的势函数可取φ1=p，φ2=q，其中λk（k=1，2）为待定系数，把φ1，φ2代入式（5.2.2）得：

此式也相当于张量普遍形式定律中取p，q为两个应力不变量。在塑性位势理论中，塑性势函数g此时为p，q的函数，则由塑性位势理论，也可得：

显然，式（5.2.4）与式（5.2.3）具有相同的形式，只是式（5.2.4）中dλ1、dλ2并不是完全独立的，而式（5.2.3）中λ1、λ2是相互独立的，因此，式（5.2.4）可作为式（5.2.3）的特例。

把p、q的定义代入式（5.2.3）可得：

由式（5.2.1）代入式（5.2.5）再代回式（5.2.3），并用矩阵形式表示则得：

进一步像传统弹塑性理论那样，把应变增量dε分解为弹性部分dεe和塑性部分dεp，则有

[De]为弹性矩阵，注意到

由式（5.2.6）代入式（5.2.7）再代入式（5.2.8）得

联立解式（5.2.9）两方程求得

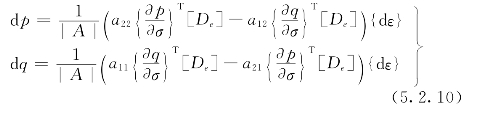
式中：

由式（5.2.10）代回式（5.2.6）后再代入式（5.2.7）可得

式中：

式（5.2.11）即为可用于有限元等数值方法的弹塑性本构方程，只要通过试验确定了式（5.2.1）中A、B、C、D4个系数，则式（5.2.11）即完全确定了，故该模型的弹塑性本构方程关键是确定这4个系数。

5.2.2 应力空间简化弹塑性模型的柔度矩阵

在应力空间，弹塑性矩阵采用柔度矩阵的形式比较简单。

根据多重势面模型理论，忽略洛德（Lode）角和应力主轴旋转等的影响，塑性应变增量与应力及应力增量的一般关系可表示为：

又因为

{dε}={dεe}+{dεp}

所以

由多重势面理论有：

由式（5.2.13）可得：

将式（5.2.12a）、式（5.2.12b）、式（5.2.14）、式（5.2.15）代入式（5.2.13）进行推导，可以得到

由弹性理论{dεe}=[Ce]{dσ}，可以得到：

则：

其中

[Ce]为弹性柔度矩阵，为塑性柔度矩阵，为弹塑性柔度矩阵：

此处采用先求出，然后通过求逆得到的方法比较简洁明了。

5.2.3 多重势面模型和塑性位势理论模型的关系

当塑性势函数g和屈服函数f为p，q的函数时，由塑性位势理论可得到其相应的弹塑性本构方程为：

式中：K为一系数；Bpp、Bpq、Bqp、Bqq为：

比较式（5.2.17）和式（5.2.11）可见，两者具有相同的形式，只是系数Akl和Bkl不同。进一步比较、）～（p、q）空间上的关系，由塑性位势理论可得：

通常塑性位势理论中的关联模型为g=f，则由式（5.2.13）有：

比较式（5.2.19）和式（5.2.1）可见，两者具有相同的形式，而式（5.2.20）相当于规定式（5.2.1）中的系数满足

非关联模型时g≠f，则：

相当于规定式（5.2.1）中的系数满足：

显然，材料的本构特性应取决于材料本身而不能人为规定，A、B、C、D4个系数最为一般的情况应是从材料的本构试验来确定，由第四章的研究成果可知，式（5.2.23）或式（5.2.21）的第一式相当于假定了塑性应变增量方向具有唯一性的数学条件[45，115]。因此，传统塑性位势理论实质上是规定了A、B、C、D4个系数满足一定的数学条件的特殊情况，而由多重势面理论所建立的本构方程式（5.2.11），其A、B、C、D可不作人为规定而直接从试验来确定，因此，塑性位势理论模型仅是多重势面理论模型的特例。通常关联模型中弹塑性矩阵为对称而便于数值计算，可以直接在式（5.2.1）中假定B=C，则相应的弹塑性矩阵由式（5.2.11）可见也是对称的，此时Apq=Aqp，若进一步假定AD-BC=0，则由式（5.2.11）中可见，Akl的表达式将进一步可简化，而应用多重势面理论则无需去推求塑性势函数和屈服函数即可直接得到弹塑性矩阵，这是其简便之处，且其还更具有一般性，也可以无需人为规定A、B、C、D系数的关系。因此，由新理论所建立的本构方程具有更多的优点。

5.2.4 多重势面模型参数的确定

现以文献[67]的试验资料来说明新模型参数的确定，并与文献[67]采用的关联模型的结果进行比较。

文献[67]中采用水坠坝冲填土进行了σ=const.和P=const.的三轴试验以及等向固结试验，并分别进行了加卸载试验。

试验用土取自广东仁化县高坪水坠坝冲填土，属砾质中壤土，黏粒含量12.0%，粉粒含量16.5%，砂粒含量41.5%，砾粒含量30.0%，比重Gs=2.63，液限ωL=32%，塑限ωp=17.7%。拌土时含水量为40%，经过析水后含水量ω=31%，此时干容重γd=1.44g/cm3。根据试验结果，按清华模型的思路方法确定屈服面、硬化参数，称其为关联模型。

5.2.4.1 弹性矩阵[De]的确定

[De]的确定可通过回弹试验来确定，具体方法可参见文献[67]，这里不再重复。

5.2.4.2 A、B、C、D系数的确定

这里假定这4个系数与应力路径无关，则可以通过三轴试验来确定，分两种情况。

（1）对A、B、C、D关系不作规定。称这种模型为EμKG模型，在式（5.2.1）中增加弹性应变K、G分别为弹性体积模量和剪切模量，则式（5.2.1）改用总应变表示为：

各参数确定如下：

1）A的确定。由等向固结试验得lnp～εv及其回弹曲线如图5.2.1所示，用下式拟合试验结果：

图5.2.1 等向固结试验及其回弹曲线

由最小二乘法求得a0=19.77，a1=4.56，a2=0.71，εv为百分数，微分式（5.2.25）得：

此时应力状态为q=0，dq=0，比较式（5.2.19）第一式得：

2）由p为常数的三轴试验确定D。对p=0.05，0.15，0.3MPa的三轴试验，采用归一化方法拟合曲线，令η=q/p，η可近似为双曲线方程

图5.2.2所示为的试验点，接近为一直线，求得a=0.6，b=0.52，微分式（5.2.28）并由式（5.2.28）解出代入得：

在p=常数应力状态下，dp=0，由式（5.2.24）第二式与式（5.2.29）比较可得

图5.2.2 归一化的应力应变曲线

3）由σ3为常数的三轴试验确定B、C。σ3为常数的常规三轴试验中，σ2=σ3，dσ2=dσ3=0，ε2=ε3，dε2=dε3=-μtdε1，μt为切线泊松比，（1+μt）dε1，dp=dσ1，dq=dσ1，μt=-dε3/dε1，Et=dσ1/dε1，Et为切线变形模量，代入式（5.2.24）可解得：

则B、C可由Et，μt而求得，Et、μt可按邓肯—张模型的方法来确定。试验得到土的黏聚力c和内摩擦角φ为c=0.01MPa，φ=37.9°，关系如图5.2.3所示，按邓肯模型方法得Et公式为：

图5.2.3 与ε1关系图

其中K=60，n=0.988，对μt，图5.2.4所示为不同σ3时ε1～ε3的关系，由图可见，其可用两段直线来表示，由μt的定义，由图得当ε≤4.8%时，μt=0.2，当＞4.8%时，μt=0.43，则A、B、C、D4个系数即可完全确定。

（2）假定B=C，称其为EμK模型。此时要确定的系数只有3个，即A、B=C和D。A的确定如上式（5.2.27）所示，B=C、D可由σ3=常数的试验来确定，由式（5.2.31）第一式，因A已知，则通过以上所得Et、μt即可得到B，由于B=C，代入式（5.2.31）式第二式解出D得：此时可不用p=常数的三轴试验，且由此所得的弹塑性矩阵是对称的，而这一模型也无需假定塑性应变增量方向具有唯一性，即不作AD-BC=0的假定，因而在一定程度上还可以反映加荷方向的影响，这是弹塑性矩阵对称的关联模型所不能反映的。

图5.2.4 不同σ3时，ε1～ε3关系

由以上方法所确定的EμKG模型、EμK模型和文献[67]采用通常的关联模型所得的结果和试验结果比较如图5.2.5、图5.2.6、图5.2.7、图5.2.8所示，由图可见新模型与试验结果具有较好的一致性，尤其是对P=常数的试验，新模型的q～结果较关联模型好些，但q～εv的模拟较关联模型差一些，这可能是泊松比μ的模拟不太好的结果，但新模型在理论上比传统的塑性位势理论模型具有更广的适用范围，且参数确定也更为简便，没有推求塑性势函数和屈服函数等复杂的工作，因而具有较好的优越性。

图5.2.5 σ3=常数时试验与计算的q～εv曲线

图5.2.6 σ3=常数时试验与计算的q～曲线

(www.xing528.com)

图5.2.7 p=常数时试验与计算的q～εv曲线

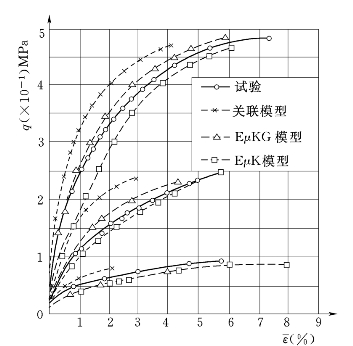
图5.2.8 p=常数时试验与计算的q～曲线

5.2.5 多重势面模型与邓肯—张模型的比较

5.2.5.1 以邓肯—张模型确定多重势面模型参数

邓肯—张E—μ模型是比较常用的模型，利用该模型中关于应力和体应变关系的双曲线假定，可以构造多重势面模型，所需参数与E—μ模型参数完全相同。

由于常规三轴试验只能提供两个等式，所以还应做出假定：

这样共有4个等式，就可以解出4个未知量A、B、C、D。

常规三轴试验中：

代入式（5.2.12），有

考虑到Et=dσ1/dε1，于是：

联立式（5.2.34）和式（5.2.35）即可得到：

其中

Ee、μ为卸载时的弹性模量和泊松比（μ一般取0.3）。

用邓肯—张的双曲线假定确定Et、μt各参数：

用上述方法建立的多重势面模型与邓肯—张E—μ模型所需参数完全相同。但多重势面模型能够反映土的剪胀性。Et、μt不受广义虎克定律的限制，当μt＞0.5时也能正常计算，而不会引起刚度矩阵的歧义。这在后面的砂土及堆石材料的计算中可见证，但此时μt的确定则要采取另外的方法。

5.2.5.2 对三轴试验的计算

（1）黏性土的计算比较[137]。为了同邓肯—张模型比较，并分析多重势面模型的特点，在此对如图5.2.9所示的三轴试验进行计算，计算中取围压σ3=100kPa，计算参数见表5.2.1。对多重势面模型，计算中Ee=KurPa（σ3/Pa）n，μe取定值0.3。

图5.2.9 所取试样单元示意图

表5.2.1 土的多重势面模型及邓肯—张模型计算参数

1）dσx=dσy=0，dσz＞0情况下的计算成果。此时即为常规三轴试验的受力条件，计算成果如图5.2.10所示。多重势面模型与邓肯—张模型对偏差应力和体应变的计算曲线几乎完全重合，表明两者计算结果非常接近。

图5.2.10 dσx=dσy=0，dσz＞0情况下的计算成果

2）dσx=dσy＞0，dσz=0情况下的计算成果。此时意味着三轴试验中轴向应力不变，而在径向两个方向施加压力。计算出的偏差应力（σx-σz）及体应变εv与εx的关系如图5.2.11所示（注意此时σx＞σz）。从图中可以看出，多重势面模型与邓肯—张模型对应力计算结果较为一致，但对应变计算结果略有差别。

图5.2.11 dσx=dσy＞0，dσz=0情况下的计算成果

3）dσx=dσy=dσz＞0情况下的计算成果。此时即为等向加压的情况，给试样施加的是球应力，计算成果如图5.2.12所示。两者计算结果非常一致。

图5.2.12 dσx=dσy=dσz＞0情况下的计算成果

4）dσx=dσy=dσz/3＞0情况下的计算成果。此时意味着轴向与径向同时加压，施加等比例的荷载，计算成果如图5.2.13所示。从图中可以看出两种模型对εv～εz的计算结果有较大的出入，其原因将在后面做分析，而（σz-σx）～εz曲线依然比较接近。

图5.2.13 dσx=dσy=dσz/3＞0情况下的计算成果

（2）砂土的计算比较[137]。砂土的模型参数如表5.2.2所示。

表5.2.2 砂土邓肯—张模型计算参数

用邓肯—张模型以及采用邓肯—张模型参数确定的多重势面模型计算了单元体的应力应变关系如图5.2.14所示。

图5.2.14 砂土的计算结果

计算表明两者对偏差应力的计算结果完全相同（因此图5.2.14中只绘出了多重势面模型对偏差应力的计算成果），但对体应变，计算参数中G=0.8＞0.5，用多重势面模型能反映土的剪胀。用E—μ模型，由于要限制μ＜0.5，所以无法反映土的剪胀，也即计算不出εv＜0的情况。多重势面模型在μ＞0.5时也能正常计算并能反映土的剪胀性，这是它别于邓肯—张模型的重要特点。而邓肯—张模型计算的εv＞0，不能反映砂土剪胀产生的负体变。

（3）堆石材料的计算比较[138]。堆石材料具有明显的剪胀性，如图5.2.15所示[56]，对于体变曲线采用沈珠江提出的抛物线拟合。

图5.2.15 堆石料常规三轴试验体变曲线

常规三轴试验得到的εv～ε1曲线，最大体应变εvm与对应的围压力σ3用指数曲线拟合，即：

式中：Cd和nd为拟合参数。

由于体变曲线过原点，可以确定整个抛物线的形状：

式中：εa为轴向应变；εam为εv=εvm时的轴向应变。

定义体积比：

对式（5.2.39）求导，得到：

以偏应力（σ1-σ3）代替εa作为自变量，并令

又定义：

其中（σ1-σ3）m为εv=εvm时的偏差应力，为（σ1-σ3）ult极限偏差应力。可以得到：

由于三轴试验条件下“泊松比μt”与体积比的关系为：

于是有：

采用邓肯—张模型和多重势面弹塑性计算常规三轴试验的受力条件，两个模型参数如表5.2.3所示，应力应变关系计算结果如图5.2.16所示，图中DC模型为邓肯—张模型，MPS模型为多重势面模型。

表5.2.3 堆石材料模型参数

从图5.2.16可以看出，多重势面模型可以较好反映土的剪胀性，而邓肯—张模型不能反映这一规律。事实上，泊松比大于0.5以后邓肯—张模型已不能正常计算，而多重势面模型不受这一约束，说明在反映剪胀性方面，多重势面具有优越性。

图5.2.16 堆石料常规三轴试验计算成果

（4）多重势面模型弹塑性矩阵的分析。若x，y，z为主应力方向，则多重势面模型的塑性柔度矩阵为：

这是一个对称阵，其中：

在三轴试验条件下：

本构关系进一步简化为：

其中：

1）σz＞σx，εz＞εx的情况。在此种情况下有：

于是对多重势面模型有：

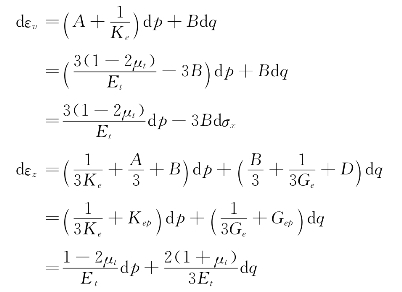
而对邓肯—张模型有：

比较在这种条件下多重势面模型与邓肯—张模型dεv、dεz的计算公式可以发现，dεz的计算公式完全相同，而dεv的计算公式中，多重势面模型比邓肯—张模型多出一项（-3Bdσx）。图5.2.10中由于dσx=0，所以两种模型偏差应力与体应变的计算结果完全一致；图5.2.13中因为dσx≠0，所以两种模型的偏差应力计算结果一致，而体应变计算结果有一定的差别。

2）σx＞σz，εx＞εz的情况。在此种情况下：

于是对多重势面模型：

而对邓肯—张模型：

比较在这种情况下多重势面模型与邓肯—张模型dεx、dεv的计算公式可以发现，dεx、dεv的计算公式都存在差别。dεx的计算公式中，多重势面模型比邓肯—张模型多出一项[-B×（dσx+2dσz）/6]，dεv的计算公式中，多重势面模型比邓肯—张模型多出一项[（-B（dσx+2dσz）]。在本节使用的计算参数下，两种模型dεx的计算结果差别最大仅为6%左右，而dεv的计算结果差别最大达到了93%左右，所以图5.2.11中两种模型偏差应力计算结果非常接近而体应变的计算结果有明显的差别。

3）施加球应力的情况。此时dq=0对多重势面模型有：

而对邓肯—张模型：

比较在这种情况下多重势面模型与邓肯—张模型dεz的计算公式可以发现，两者的计算公式相同，所以图5.2.12中两种模型应力计算结果是相同的。

4）μ＞0.5的情况。当μ＞0.5时，对邓肯—张模型，由于此时违背广义虎克定律，使矩阵的主对角线元素小于0，所以无法正常计算。多重势面模型却能始终保证主对角元素大于0。记为：

可以得到式（5.2.12）中

可以证明，实际上β=1/Et-1/Ee，一般总大于0，所以多重势面模型能够保证主对角元素大于0，因而当μ＞0.5时也能正常计算。

5.2.6 小结

本节在多重势面理论基础上建立了应力空间上的简化多重势面弹塑性本构模型，这一模型在表述材料本构特性上比传统的塑性势理论模型更具有一般性，同时参数确定也比传统的塑性位势理论模型更为简便，没有了推求塑性势函数和屈服函数的复杂工作和困难。经与试验结果比较，模型也可以反映不同应力路径的结果，与关联模型比较，不但参数确定更为简便，且结果也较好。

通过数值计算表明，应力空间的简化多重势面弹塑性模型在表述土的剪胀性方面具有较好的优越性，其参数可以像邓肯—张模型那样简便，但可以表述泊松比μ＞0.5的情况，也即可以更好地反映土的剪胀性。