弹性势理论的数学实质：土的本构模型的广义位势

（1）传统弹性势理论的建立[42，109，133]。对弹性材料，假设应力可唯一地表示为应变的函数，即有：

设物体在平衡状态下产生很小的虚位移δui，即Ti为作用于物体表面的外力，Fi为体积力，相应的应变增量为δεij，则由虚功原理有：

式（4.3.2）中等式左边表示外力所做的虚功，右边为弹性应变能贮存于物体中，记为另一种形式：

式中：W称作为单位体积中的应变能或应变能密度。由式（4.3.3）有：

由于假设应变能W仅是εij的函数，则又可有：

比较式（4.3.4）和式（4.3.5）可有：

式（4.3.6）就是从能量角度考虑所导出用于表示材料应力应变关系的弹性势理论。同理，由应变余能函数Ω，则可得另一位势函数形式的关系：

因此，传统弹性位势理论是从能量角度上得到的，但在应用时，如何确定势函数W、Ω，什么样的材料或在什么样的条件下可判别其是满足弹性位势理论的条件的，这就需要对其数学实质进行研究。

（2）弹性势理论的数学实质。如上所述，应力应变关系的试验一般可在主空间上实行并拟合，然后通过数学变换转为一般坐标空间上的本构关系，设主空间中得到的本构关系为：

或(https://www.xing528.com)

用数学上的矢量场理论分析上式，设主应变空间上一应力矢量为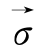=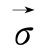（σ1，σ2，σ3），由数学上的有势矢量场的数学条件可知，该矢量的旋度恒为零时，即满足：

由式（4.3.8）代入即为：

则从数学的矢量场理论可知，σi为一有势场的矢量，存在一势函数W，使

同理，把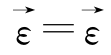（ε1，ε2，ε3）看作为一矢量场，当其主空间上的本构关系式（4.3.9）满足有势场的数学条件时，则由数学矢量场理论同样可直接得到：

再假设σi和εi（i=1，2，3）的3个主量方向相同时，则由以上用导数表示的坐标变换关系有：

或

分别代入式（4.3.12）和式（4.3.13）则得：

此即为以上传统理论中从功能角度上得到的弹性位势理论，而这里则是直接从数学角度出发所得到，说明传统的弹性位势理论其数学实质是假定了其主空间上的本构关系矢量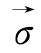或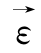为一有势场矢量，且σij和εij的3个主方向是一致，这是从传统的功能角度上来建立的本构理论所不易揭示到的数学实质，显然，若主空间上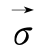或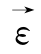不满足有势场的数学条件，则这样的本构关系用传统的弹性位势理论是不能表述的，此时可以应用上面的广义位势理论之多重势面理论或张量普遍形式定律来表述。

因此，弹性理论的数学实质是应力主量或应变主量为一有势矢量，且主应力的3个主方向与应变的3个主方向相同。