土的本构模型的广义位势理论及应用：数学实质与成果

首先从数学角度上来考察一下塑性位势理论，传统塑性位势理论在一般坐标空间中表示为：

式中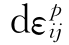：为塑性应变张量增量；Q为塑性势函数。在主空间中，式（4.1.1）退化为：

如果我们把作为一矢量，则在主应力空间中，式（4.1.2）表示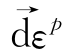ε的方向与应力增量矢量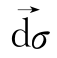无关，仅决定于应力状态σi，同时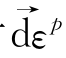的方向为一有势场的方向，此时式（4.1.2）表示的是主空间上的一个张量方程。因此，从数学角度上，塑性位势理论只是假定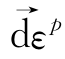为主应力空间上一矢量，这一矢量方向与应力增量dσi无关，且该矢量的方向为有势场的方向。目前的一些试验表明，并不是所有材料其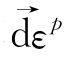的方向都与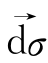无关的，一些土体的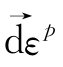的方向是与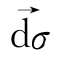有关的[10，118]。

为更清楚地了解塑性位势理论的数学实质，我们可从一般情况来作一探讨，设主空间上塑性应变增量与应力增量的一般关系为：

aij为应力总量σi或应变总量εi或应力路径等的函数。文献[45]已对[A]的特性从数学上进行了探讨，当[A]的秩为1时，则从数学矢量场理论可知，[A]只有一个基向量，且存在一三维矢量（α1α2α3）和3个系数β1、β2、β3，[A]可以表示为：

代入式（4.1.3）有：

即

其中：

则此时由式（4.1.5）可有：

βi（i=1，2，3）为σi或εi的函数，则式（4.1.6）表示塑性应变增量矢量的方向与dσi无关，也即通常所说的塑性应变增量方向具有唯一性的假设，显然，这一假设从数学上看，则相当于假定式（4.1.3）中的矩阵[A]的秩为1，而材料本构关系矩阵[A]的秩是否为1，应取决于材料本身的力学特性，而不能人为设定，因此，作为一种假定并不一定都适用于所有的工程材料，这也是传统塑性位势理论的一个假设，可作为一种特殊的情况。若进一步假定矢量为一有势场，即存在一势函数Q，使

则代入式（4.1.5）即得：(www.xing528.com)

这个方程在一般坐标空间中，当假定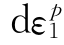与σi的3个主方向相同时，由第三章可知，通过数学变换可得：

此即为从数学上导出的经典塑性位势理论的形式，这一关系其实质也包含了塑性应变增量3个主方向与应力3个主方向一致的假定。

从以上可见，经典塑性位势理论从数学上假定[A]的秩为1和矢量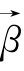为一有势场，简单地说，从数学上，塑性位势理论就是假定塑性应变增量矢量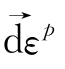在应力空间上其方向为一有势场的方向，从而可以用一势函数的梯度矢量来表示这一方向。这是传统的塑性位势本构理论的数学实质，如果从所揭示的这一数学实质出发，则很容易可以得到上一章的单一势面广义塑性位势理论，如假定塑性应变增量矢量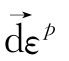在主应变空间中是一有势场方向，根据上面的结果即可有关系：

再假定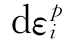3个主方向与σi的3个主方向相同，则由第三章的结果可得：

上式在传统的塑性位势理论中是没有的，但若从以上的数学假设出发则很容易得到，且由此出发所得到的理论其数学原理很明确，对所采用的数学假定也是很清楚的。同理我们也可以得到在应变空间上表述的与依留申公设所得到的一致的应变空间塑性位势理论。

另一方面，从数学原理也可进一步考察金属材料是否满足塑性位势理论的数学条件，金属材料的试验表明，塑性体应变dεpv与静水压力dp无关，本构关系可忽略π平面上的影响，则其塑性本构关系用不变量可表示为：

则A=0，B=0，C=0，系数矩阵的秩为1，塑性矢量的旋度满足

的条件，因此，金属材料的塑性本构关系是满足传统塑性位势理论的数学条件的。

再者，若式（4.1.3）中矩阵[A]的秩大于1时，显然传统单一塑性位势理论是不能表述的，则此时需要应用前面的多重势面理论。