张量普遍形式定律：土本构模型的广义位势理论及应用

以上从坐标变换的导数表示方法建立了势函数形式的本构理论——广义位势理论，本节从张量角度出发建立可普遍适用的本构方程，可以像势函数形式的理论一样，用于建立材料本构模型时同样具有普遍性。

普遍形式定律：如果一个二阶对称张量Aij的3个主方向与另一个二阶对称张量Eij的3个主方向相同，则这两个二阶对称张量有以下形式的张量关系方程：

或

式中：Aij，Eij为其张量分量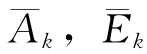；（k=1，2，3）为其任一种形式的3个张量不变量；λk，μk（k=1，2，3）为3个待定系数。

证明如下：

（1）由张量分析，二阶对称张量Eij的3个不变量的一种形式为：

任何一种形式的3个不变量均可以由另一种形式的3个不变量来唯一地表示，由式（3.6.3）可得：

（2）二阶张量的幂关系[116]。若a是二阶张量[T]对应的主值λ的特征向量，即：

则有：

[T]n表示[T]的n次幂，n次幂后仍是二阶张量，且二阶张量[T]的n次幂[T]n与[T]的主方向相同，[T]n的3个主值也是[T]的相应3个主值λ1，λ2，λ3的n次方，即为，，。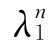

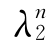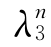（3）因假定Aij与Eij有相同的主轴方向，显然Eij的主轴空间与Aij的主轴空间是重合的，在主轴空间中Aij，Eij都仅有3个主值，设为A1、A2、A3和E1、E2、E3，在Eij的主轴空间中，可把A1、A2、A3看作为一个三维矢量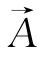=（A1，A2，A3）的3个分量，由线性代数理论，在这主空间上可以选择3个线性无关的矢量来线性地表示，由上可知，单位二阶张量[I]、[E]及[E]的二次幂[E]2具有相同主轴方向，即是同一主轴空间上的3个量，且[I]、[E]、[E]2的3个主值组成的矢量线性无关，因此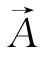，的3个分量可由其唯一地线性表示：

式中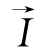：=（1，1，1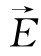），=（E1，E2，E3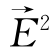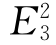），=），式（3.6.5）展开为：(www.xing528.com)

α、β、γ为3个待定系数，式（3.6.5）和式（3.6.6）代表了主轴空间上的一个张量方程：

由于张量方程在任何坐标系空间中均成立，故在一般的坐标空间中，式（3.6.7）也成立，此时展开式（3.6.7）则有：

由式（3.6.4）代入则得：

令采用张量求和约定写法，则式（3.6.9）可简写为：

由于二阶对称张量的任一种形式的3个不变量均可以由另一种形式的3个不变量唯一地表示，因此，任一种形式的不变量都可唯一地表示为另一种形式不变量的函数，将其代入式（3.6.10），应用复合函数求导法则，则可以得到式（3.6.1）的一般形式，同理可证得式（3.6.2）成立。

如果式（3.6.1）、式（3.6.2）中取3个不变量E1、E2、E3和A1、A2、A3分别为二阶张量的3个主值，则在主轴空间中，Eij=0（i≠j），Aij=0（i≠j），此时有

代入式（3.6.1）、式（3.6.2）即得在主轴空间中有：

对一般的直角坐标系，把在这一条件下识别的系数λk，μk代回式（3.6.1）、式（3.6.2）则得：

以上也曾直接从导数表示的坐标变换关系得到了类似式（3.6.11）、式（3.6.12）的 形 式，如 式（3.3.17）和 式（3.3.18）所示，并揭示了势函数形式的本构理论在数学上实质是一个特定条件下的坐标变换。说明不同途径得到了相同的结果。

如果假定Aij、Eij分别为应力张量σij和应变张量εij，则式（3.6.1）、式（3.6.2）即是本构方程的一种较为普遍的形式，称其为普通形式定律，目前的一些模型理论，如塑性位势理论、弹性位势理论、广义虎克定律等都可作为其特例而得到，多重势面理论的结果与此也是一致的。