广义位势理论及其在土壤本构模型中的应用

上节用导数变换法来建立一般坐标空间的本构关系，并已应用于建立势函数形式的本构理论，本书中把这种利用数学上的势函数方法来建立本构模型的理论称为广义位势理论。其实当主空间上的本构关系是一有势场或其方向是有势场的方向时，通过导数表示均可以得到一般坐标空间下的势函数形式的本构理论——单一势面理论。

3.4.1 全量式单一势面理论

已由上节导得如式（3.3.31）和式（3.3.33）所示，即当主空间上有：

或

同时假设σk和εk的3个主方向相同时，则由上节结果可有：

或

其结果为超弹性理论中的弹性势理论。

3.4.2 广义塑性位势理论——单一势面塑性位势理论

上节所得到的式（3.3.54）、式（3.3.57）、式（3.3.61）和式（3.3.62）即构成了广义塑性位势理论的4个正交流动法则，笔者在文献[111]中则直接把传统正交流动法则的数学思想推广而得到了以上的4个关系，后来又从数学的角度上推导得到[106]，为便于表示和推导其弹塑性应力应变关系，统一表示为：

其中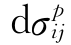与的关系服从弹性关系[28]

以上4个正交关系中，式（3.4.5）为传统塑性位势理论的流动法则，式（3.4.8）则是通常应变空间上的流动法则，而式（3.4.6）、式（3.4.7）则是以前一般教科书中所没有的，但文献[69]曾采用过与式（3.4.6）类似的公式来推导和建立塑性本构关系。

3.4.3 关于塑性状态方程或屈服函数的合理确定问题(www.xing528.com)

有了流动法则，要建立合理的弹塑性模型时通常还要求取一个屈服函数，用于确定式（3.4.5）～式（3.4.8）中的比例系数dλ1、dλ2、dλ3和dλ4。

材料的屈服是其有无塑性变形的判断准则，很多试验已表明，大多数土并不只有唯一的屈服面，由于其剪切时的摩擦特性和在等向应力下的颗粒移动的塑性变形，土在卸载—再加载时也存在塑性变形，并且土的屈服也与一定的应力路径有关，这就使土的屈服面呈十分复杂的形式。也有人企图通过不同应力路径试验直接确定土的屈服面，也有人在Drucker假设的前提下通过确定塑性势面从而认定为屈服面，但都不是十分成功。关于土的屈服面形状是否唯一，以及是否与应力路径有关，成为土力学中重大的悬案，所以现有的土的弹塑性模型的屈服都是假设的：它一般是塑性应变的函数，并且塑性应变（硬化参数）支配其变化。从另一角度讲，若设塑性应变全量εp与应力全量σ间存在对应关系，则塑性状态方程本身也就可作为屈服面。并且无需人为假设，因为它毕竟可以通过一定试验来明确地确定。

作者在文献[112]提出了用塑性状态方程的概念来取代屈服面的概念以确定流动法则的比例系数dλ。所谓塑性状态方程是指塑性应变εp与应力σ关系所满足的方程，假设εp与σ存在对应关系时，可以通过用数学方法拟合试验数据而得，如在主空间上

塑性状态方程的概念与屈服面的概念是不同的，塑性状态方程是数学拟合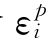～σi关系的数学方程，其函数形式可以是多样的，可以人为选择，如式（3.4.10）左边也可以取为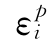的函数，则fi相应也可以变化，而作为屈服函数是作为判别材料是否发生塑性应变的一个准则，对于一定的材料在一定的条件下应具有唯一性，因而对无明显屈服点的土体材料屈服面的确定比塑性状态方程复杂得多，而塑性状态方程可不受屈服概念的限制，容易确定，但很难证明其唯一性，当然，屈服函数也可作为其中的一种塑性状态方程，因它也是εp与σ所满足的一个方程。实质上这里定义的塑性状态方程的概念与文献[113]所定义的屈服面随硬化规律的假定不同，而不同的观点具有异曲同调之意，只是这里为避免屈服概念的限制而称之为状态方程。

从数学角度，对一个矢量已知其方向和模长即可唯一地确定了，对于符合单一势面流动法则的材料，势函数已规定了这个矢量的方向，塑性状态方程的目的就是用于确定这一矢量的模，设塑性状态方程为：

微分上式，则有：

以式（3.4.5）的流动法则为例来代入上式可得dλ1为：

把dλ1代回式（3.4.5），写成矩阵形式则得：

当在主空间时，上式同样成立，而在主空间中可由试验直接得到：

显然，在主空间上式（3.4.14）能否全面代表式（3.4.15），此时塑性状态方程S或通常的屈服函数F的选择就值得研究了。通常S函数也可写成S（σij，H）=0，H为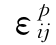的函数，当S为屈服函数时，H就是通常的硬化参数。这时，选择H的不同函数形式相应的S函数形式也就不同，反之，选择不同的S时，其相应的H也将是不同的，但作为状态方程，要求是满足式（3.4.11）。显然，当选择S=Q1时，即得到通常的关联流动模型，此时塑性矩阵是对称的，当S≠Q1时，即得到通常的非关联流动模型，合适的S函数的选择应使式（3.4.14）的塑性矩阵和式（3.4.15）中的[A]矩阵相同，当两者不同时，其反映的力学特性是不同的，在特定应力路径下则只是一个等效模型，当应力路径不同时，势必会产生误差。当[A]为对称矩阵时，选择S=Q1则是唯一的，而当[A]为非对称矩阵时，则S的选择应要根据[A]的性质来确定，因单一位势理论成立时，[A]的秩为1，则[A]可以分解为两个矢量的积[45]：

{α}代表了dεp的方向，相当于Q1的梯度方向，而S函数或屈服函数的选择则同样应使其梯度方向与{β}的方向相一致，这样才是合理的非关联模型，后面将对此作进一步的分析。而目前的非关联模型中在合理选择屈服函数方面对这一点则研究得是不够的，若屈服函数按文献[113]的观点是可变的或按本文的观点用塑性状态方程代之才可有调节的可能性，但这种选择是复杂的。本书在后面的章节中，在新理论基础上建立的模型将可以克服非关联模型中合理确定状态方程或屈服函数所遇到的这个难题。因此，在应用单一势面理论时，必须注意所建的模型是否能真正反映材料的试验结果和力学特性，尤其是所谓的非关联模型中，塑性状态方程或屈服函数的合理选择是需要研究的。