导数表示变换法-土本构模型位势理论应用

3.3.1 导数表示的变换法

设两直角坐标系ox′y′z′和oxyz各轴的方向余弦如下表所示：

则两坐标的应力分量间的变换关系为[107，108]：

其中：

σij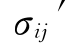，分别为x、y、z和x′、y′、z′坐标系下的应力张量：

如果x、y、z三坐标轴的方向与3个主应力σ1，σ2，σ3的3个方向重合，则由式（3.3.1）、式（3.3.2）可有：

σ11=σ1，σ22=σ2，σ33=σ3，由式（3.3.4）则可得：

令

同时注意主应力σk（k=1，2，3）既是σij又是σij′的主应力，因此，σk既可以表示为σij的函数，又可以表示为σij′的函数，将式（3.3.5）、式（3.3.6）代入式（3.3.3），并把σkk简记为σk（k=1，2，3）则有：

同理有：

对于应变张量，我们同样可以得到：

则式（3.3.8）、式（3.3.9）即为导数表示的坐标变换关系，这是从数学角度直接得到的。此外，也可以从坐标变换的矩阵表示来推导出以上导数表示的坐标转换关系。两坐标的应力分量间的变换关系为：

式中：=[σx σy σz τxy τyz τzx]T。

当x、y、z三轴方向与3个主应力的方向σ1、σ2、σ3重合时，则有：

其中{σi}3×1=[σ1 σ2 σ3]T，则由式（3.3.13）可得：

令

考虑τij′=τji′（i≠j），故式（3.3.14）中对τij′（i≠j）的偏导数项中是包含了对τij′和τji′（i≠j）求导之和的，例如：

对应式（3.3.13）项应为：

由于τxy′=τyx′，故而第4项为2l1l2τxy′，这样式（3.3.14）中对剪应力τij′（i≠j）项的导数实际上是两项之和，如由式（3.3.16）则应为：

即

因此，把式（3.3.14）代回式（3.3.12）并考虑式（3.3.17）或式（3.3.18）的情况，则式（3.3.12）又可表示为：

用张量符号表示上式则为：

此即为以上的式（3.3.7），这里只是详细展开的结果。

由此，如果我们能由三轴试验得到主空间的本构关系，则可以直接由式（3.3.8）、式（3.3.9）得到张量本构方程。例如，假定我们可以得到主空间上的3个本构方程为：

或

则由式（3.3.21）代入式（3.3.8）得：

同理由式（3.3.22）、式（3.3.9）得：

显然，式（3.3.23）右边的导数仍含有应力分量，式（3.3.24）右边同样含有应变分量，这种两边均含有待求量的本构方程在实际应用时不够方便，为此，可以假设3个主应力的方向与3个主应变的方向相同，则有：

则由式（3.3.25）分别代入式（3.3.23）、式（3.3.24）即可得：

此两式的右边不含左边的待求量，应用较方便。

由此，根据以上对二阶张量应力张量和应变张量的数学分析，我们可以得到一个重要的本构定律：

如果二阶对称张量Aij的3个主量Ak（k=1，2，3）的3个方向和另一个二阶对称张量Bij的3个主量Bk（k=1，2，3）的3个方向相同，则有关系：(www.xing528.com)

因应力张量和应变张量均为二阶对称张量，因此，式（3.3.28）、式（3.3.29）的形式则可以普遍地用于建立材料的本构方程。

3.3.2 导数变换方法及其势函数理论

如果式（3.3.21）的三个函数刚好是一个势函数的3个偏导数，即是一个有势场，则存在一势函数ψ（ε1，ε2，ε3），使

代入式（3.3.26），则可得：

同理，若式（3.3.22）是一个有势场，即存在一势函数φ，使

则代入式（3.3.27）得：

显然，式（3.3.31）、式（3.3.33）即是所谓的超弹性本构理论的关系式。以往的论著中，这两个关系式是通过物理上的功能概念而得到的[109]，这里则直接从数学方法得到，对其引入何种数学假设可得到一个清晰的认识，就是要求主空间上的本构方程是有势场，且主应力与主应变的3个方向相同，而按以往的方法导出则是不易认清其所采用的数学假设的。

3.3.3 增量形式的导数变换方法及其势函数理论

对于增量分量组成的应力张量Δσij或应变张量Δεij，当假设二者的3个主方向一致时，根据式（3.3.28）、式（3.3.29），则有：

同样，如通过主空间上的应力—应变试验而得到了主空间上的本构关系

或

代入式（3.3.34）、式（3.3.35）即可以得到增量形式的本构方程。如进一步假定增量的3个主方向与全量的3个主方向相同，则式（3.3.34）、式（3.3.35）又可以写成以下的形式：

显然，如果式（3.3.36）、式（3.3.37）是有势场或其方向是有势场，即若

成立，其 中dλ、dμ为 系 数，分 别 代 入 式（3.3.34）、式（3.3.35）、式（3.3.38）、式（3.3.39），则可以得到势函数形式的本构方程：

3.3.4 增量弹塑性的势函数理论

按经典增量弹塑性理论一样，把总应变增量Δε分解为弹性应变增量Δεe和塑性应变增量Δεp，与Δεp对应的应力称为塑性应力增量Δσp。由以上定律式（3.3.28）、式（3.3.29），则很易建立弹塑性的势函数本构理论，这里主要讨论塑性关系。弹性本构关系同样可建立，也可以像弹性理论那样建立。与上面增量理论一样，假定塑性应变增量的3个主方向与应力增量的3个主方向一致，则有：

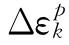可以由主空间中的本构试验得到，假定表示为σk、Δσk的函数

将式（3.3.49）代入式（3.3.48）即得到塑性本构关系的张量方程。若式（3.3.49）式满足下式，即：

dλ为比例系数，代入式（3.3.48）即得：

同理，若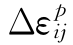的3个主方向与σk的3个主方向相同，则有：

同时，若主空间上的方向为有势场，即：

将其代入式（3.3.52）即有：

此即为经典塑性本构理论中的塑性位势理论，本文在此直接从数学角度而得到，与传统塑性位势理论提出的依据不同。同时，由上可见，塑性位势理论的成立，其主空间上的本构关系必须满足式（3.3.53）的要求，由此式可知，主空间上塑性应变的增量方向与应力增量的方向无关，在此条件下，由塑性公设同样可以得到式（3.3.54）的形式，但此时ψ同时为屈服函数。同时，由式（3.3.52）可见，塑性位势理论在数学上还对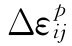的主方向作了假设的，即假定了塑性应变增量的3个主方向与应力全量的3个主方向一致的。

同样，我们可以在应变空间上来建立塑性本构关系，由式（3.3.28）或式（3.3.29），假定塑性应变增量张量的3个主方向与应变全量张量的3个主方向相同，则有：

若在应变主空间上Δεpk的方向是有势场，则：

代入式（3.3.55），则有：

类似式（3.3.50）同样可有：

以上一系列公式构成了应变空间上的塑性位势理论，笔者在文献[111]中曾提出了式（3.3.54）、式（3.3.57）这样的形式，由式（3.3.57）可见，该形式与从塑性公设建立的应变空间理论是不同的。同理，若以塑性应力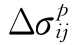来建立塑性本构关系，在以上假定的数学条件下可有其势函数形式的本构方程：

此即为应力空间上的塑性位势理论，其中式（3.3.61）即为与由塑性力学中按依留申公设所得到的应变空间中位势理论的形式一致，但此时φ必为屈服函数。而式（3.3.57）则是从数学角度上得到的，其形式与式（3.3.61）显然不同。同时，式（3.3.62）也是传统理论中所没有的。由此，通过导数形式表示的坐标变换关系，可以建立更为系统的塑性位势本构理论，这些成果都是通过数学方法得到的，其数学原理明确，引入的数学假设清晰，且建立的理论更为广泛和一般性，而传统的塑性位势理论只是其中的部分成果。

3.3.5 小结

经典的弹性位势理论是从功能概念出发而得到的，塑性位势理论则是类比弹性位势理论而提出的，并未揭示出其数学实质。本书则直接从数学角度出发，首先建立了用导数表示的坐标变换关系，在此基础上建立了系统的、更为广泛的势函数形式本构模型理论框架，经典位势理论仅只是其中的一部分，揭示了位势理论实质上也是数学上的坐标变换关系，由此而可以把势函数形式的本构理论建立于数学基础之上。