土的本构模型：广义位势理论及应用

建立土的本构模型的关键问题仍是透彻地了解土的应力应变的机理及规律，各种试验手段、微细观的研究工作是不可缺少的。在了解其变形规律基础上进行合理的简化是本构模型的主要任务。但就实际应用的角度上，目前建立土的本构模型，目的是用于数值计算分析，通常数值计算所需要的本构关系为增量形式：

式中：{dσ}、{dε}为一般坐标空间下的应力和应变增量分量；{dσ}T=[dσxdσydσzdτxydτyzdτzx]T；{dε}T=[dεxdεydεzdγxydγyz dγzx]T；[Dep]为一个六阶矩阵，则本构模型建立的关键是如何合理确定矩阵[Dep]6×6。

显然，我们是很难直接由六维空间中的应力—应变试验去测定矩阵[Dep]6×6的，我们通常能做而又较现实的做法则是在假定土是各向同性的前提下，确定三维主空间中的应力应变关系：

式中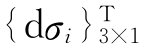：=[dσ1，dσ2，dσ3]T，{dεi}T=[dε1，dε2，dε3]T分别为3个主应力增量和3个主应变增量。

若由试验得到了式（1.4.2），则剩下的问题是如何由式（1.4.2）求得式（1.4.1），这就是各种不同本构理论需要解决的问题。由试验确定式（1.4.2）的方法，通常是由拟合应力总量{σi}和应变总量{εi}的关系，然后通过微商的方式获得其增量关系，这就存在一个如何拟合试验曲线的问题。再者，由于影响{σi}～{εi}关系的因素众多，各种组合的情况也很多，实际试验中也较难在三维空间全面的进行各种试验来反映所有的影响，因此，实际中由简单试验代替复杂试验其结果的差异也是需要研究的问题。

另一个问题则是加、卸载的问题，由于土体在加载和卸载时的应力应变关系是不同的，要在试验基础上建立加、卸载准则，亦即判别什么时候用加载的本构关系，什么时候用卸载的本构关系。(www.xing528.com)

总结以上分析，目前在反映土的主要变形特点基础上建立土的本构模型需要解决以下几个问题：

（1）由主空间本构关系到一般坐标空间本构关系的转换问题，由此构成了各种不同的理论。

（2）如何合理确定主空间的本构关系，包括如何用数学方法拟合试验结果和用什么样的简单试验来确定参数。

（3）加、卸载准则的建立。

在以上这几个问题中，传统理论中关键是第一个问题，传统理论在解决这个问题时引入的一些假设是基于金属材料试验结果上，对于岩土材料不一定都是合适的[10，134]，因而有必要去发展更为一般的理论。