民用建筑暖通空调设计气象参数导则

7.2.1　基本体系

针对暖通空调设计中不同的场景，共提出7种设计日参数，每种设计日数据根据参数的不保证水平也对应有3种不保证水平，具体如下所示：

（1）夏季干球温度及同时发生的湿球温度设计日。

（2）夏季含湿量及同时发生的干球温度设计日。

（3）夏季焓值及同时发生的干球温度设计日。

（4）冬季空调干球温度设计日。

（5）冬季供暖干球温度设计日。

（6）冬季含湿量及同时发生的干球温度设计日。

（7）冬季焓值及同时发生的干球温度设计日。

7.2.2　研究思路

7.2.2.1　现行规范设计日构造的局限

在1987年版暖通规范中，为适应按不稳定传热计算空调冷负荷的需要，在原版（1975年版）规范的基础上增订了夏季空调室外计算温度逐时化方法。编制组通过对国内外气温日变化趋势相关研究的细致分析，提出以反映温度变化与纬度、水陆分布指数和云量关系的理论公式为基础，按照气温日较差的不同将全国气温日变化情况分为3种类型。同时考虑到工程使用的简便性，基于对使用误差的充分评估，最终确定以3种基本类型气温日变化系数的定时平均作为全国通用的逐时变化系数，其结果一直沿用至今。在当时数据条件相对匮乏的情况下，编制组基于理论方法在保证一定精度的前提下确定了全国通用的逐时变化系数，为设计日在工程上的应用和推广做出了贡献。然而，随着暖通空调技术的发展，空调系统的精细化设计需求逐渐提高，如冬季采暖系统的间歇运行、夏季的冰蓄冷空调等，都需要精确的24 h的逐时化室外设计气象参数。在此背景下，现行规范设计日构造开始展现出一定的局限性。这种局限性具体表现在3个方面：一是现行规范只关注干球温度的日变化规律，而将湿球温度简单视为恒定值。随着建筑新风负荷占比的提高，湿球温度作为影响其负荷计算的主要气象要素，其日变化规律的探索也是极为必要的。二是现行规范所提供的逐时变化系数是基于理论方法确定的，对地区实际气温日变化特征的反映可能有所不足。当前气象观测数据的精度和丰富度都有显著提高，在此条件下根据实际气象观测数据的统计规律确定逐时变化系数，将能够更真实地反映气象要素的日变化特征。三是全国共用一套逐时变化系数，忽视了我国不同地域的气候差异性。考虑到使用的简便性，现行规范对全国气温的日变化趋势进行了统一描述。随着计算机技术的发展，数据的存储和调用变得方便、快捷，使得为不同城市定制个性化的设计日数据成为可能。

7.2.2.2　聚类思想的应用

设计日构造的关键是确定气象要素的典型逐时变化趋势，即规范中的逐时变化系数。现行规范所采用的温度日变化系数是基于理论方法确定的，在当前数据较为丰富的情况下，基于实际气象观测数据确定气象要素的逐时变化系数，其结果将能够更真实地反映地区实际气象要素的日变化特征。对若干典型城市的实际气象观测数据进行统计分析，其结果表明极端月内气象要素的真实日变化情况存在多趋势共存的现象，且没有表现出明显的可识别规律。为了解决这一问题，决定借鉴大数据分析理论中的聚类分析思想，从长期实际气象观测数据中提取气象要素的典型逐时变化趋势。聚类分析，简单来说就是指对数据库中无规律的对象进行分类挖掘，把分类对象按照数据自身特点分成若干类，其方法特点与设计日研究目的较为契合。为了选择合理的聚类方法，对比了在若干典型城市中采用不同聚类方法提取气象要素的典型逐时变化趋势的结果，最终认为K-Means聚类方法较为符合设计日研究的需求，能够在花费较少计算时间的前提下保证结果精度满足要求。

7.2.2.3　与室外计算参数的配合

设计日生成的实质是以室外计算参数为峰值，借助逐时变化系数展开得到一天24 h的逐时气象数据。因此，设计日数据的体系需要与室外计算参数体系相对应。为此，本标准共提供7种设计日数据，每种设计日数据有3种不保证水平。同时，本标准中大部分室外计算参数是以主、辅参数组合的形式提供的。考虑到主、辅参数在发生时间和日变化趋势上均存在一定的相关性，在参数逐时变化趋势提取的过程中，一定程度上考虑了主、辅参数逐时变化趋势在时间上的耦合关系。

7.2.3　生成方法

设计日生成可简单划分为逐时变化系数的生成和设计日的构造两个部分。

首先是基于聚类方法生成气象要素的逐时变化系数。本研究以30年的极端月（冬季12—1月，夏季7—9月）气象数据为基础，借助参数日峰值、日均值等提取所有真实日的气象要素逐时变化趋势，并根据不同主、辅气象要素的组合构建系数矩阵。在此基础上，采用K-Means聚类方法对系数矩阵进行分析，提取得到组合中主、辅参数对应的典型逐时变化特征，并转化为对应的逐时变化系数。

其中，在根据特定参数提取所有真实日气象要素的逐时变化趋势的过程中，根据设计日构造差异将气象要素逐时变化趋势的数学描述分为以下3种：

（1）基于日峰值、日均值提取气象要素的逐时变化趋势：

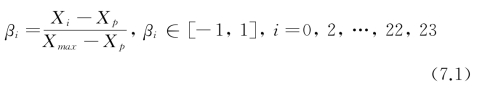
（2）基于日均值、日较差提取气象要素的逐时变化趋势：

（3）基于日谷值、日均值提取气象要素的逐时变化趋势：

式中　βi——气象要素的逐时变化趋势；

i——时刻，h；

Xi——逐时值；

Xp——日平均值；

Xmax——日峰值；

Xmin——日谷值；

Xrange——日较差；

Yp——辅参数日均值。

根据上述分类，本标准中7种设计日组合对应的气象要素逐时变化趋势提取的公式见表7.4：

表7.4　气象要素逐时变化趋势提取公式表

在聚类分析前，需要首先将提取的真实日气象要素逐时变化趋势以天为单位整理成系数矩阵。对于包含两种气象要素的设计日，考虑到主、辅气象要素日变化趋势的耦合关系，还需要将主、辅参数的系数矩阵按序组合成一个矩阵，具体如下所示：

式中　——主、辅参数逐时变化趋势；

n——天数。

在系数矩阵的基础上，采用K-Means聚类方法提取系数矩阵中各气象要素的典型逐时变化趋势，具体步骤如下：

（1）在输入数据中随机选取K个对象作为初始聚类质心Cj（1≤j≤k）。

（2）计算每一个对象βi（1≤i≤n）到所有类质心Cj的欧式距离，计算公式如下：

（3）以欧氏距离最短为依据，将每一对象分别划分到所属的类中。

（4）对每一类Cj（1≤j≤k）中的所有对象取平均值作为新的类质心。

（5）重复上述步骤直至类质心不再变化，最后将聚类结果中权重占比最高的一类的类质心所代表的气象要素逐时变化趋势作为典型逐时变化特征（βmain，βvice）。

为了保证设计日的生成是以室外计算参数为峰值点展开的，需要将主参数峰值发生时刻对应的主、辅参数的典型逐时变化趋势系数值转换为1，具体方法如下式所示：

式中　——主、辅参数逐时变化系数；

βmain，i，βvice，i——基于聚类方法提取得到的主、辅参数典型逐时变化趋势；

I——主参数日峰值发生时刻；

βmain，I，βvice，I——主参数日峰值发生时刻下，基于聚类提取得到的主、辅参数典型逐时变化趋势对应的系数值。

在计算得到设计日中各气象要素的逐时变化系数，即可根据室外计算参数生成设计日数据，具体方法见表7.5：(www.xing528.com)

表7.5　设计日生成公式表

注：式中，Xi——主参数设计日逐时值；
Xdesign——主参数设计值；
Xp——主参数日均值；
Xrange——参数日较差；
Yi——辅参数设计日逐时值；
Ydesign——辅参数设计值；
Yp——辅参数日均值。

7.2.4　典型城市的案例分析

根据项目组提供的不同热工分区典型城市的30年逐时气象数据，结合本导则的设计日生成方法，分别以夏季干球温度及同时发生的湿球温度设计日、冬季供暖干球温度设计日为例，介绍设计日的生成过程，同时与现行规范设计日进行对比。其中，所选用的设计日案例对应的典型城市如表7.6所示。

表7.6　案例城市信息表

7.2.4.1　夏季干球温度及同时发生的湿球温度设计日——以武汉、南宁为例

（1）夏季干球温度和同时发生的湿球温度的逐时变化趋势的聚类分析

在本研究设计日构造中，逐时化系数是基于实际气象数据中气象要素的典型逐时变化趋势转换而成的。为了获取武汉、南宁地区的夏季干、湿球温度的典型逐时变化趋势，首先从武汉、南宁地区的30年逐时气象数据中选取每年的7～9月的干、湿球温度数据，以日为单位从温度数据中提取干、湿球温度的逐时变化趋势，然后构建干-湿球温度系数矩阵。以该系数矩阵为基础，采用K-Means聚类方法对武汉和南宁地区的干、湿球温度逐时变化趋势进行聚类分析，结果如图7.1和7.2所示。

由图7.1中可见，武汉地区的干、湿球温度逐时变化趋势可聚成4类，其中第四类无明显变化规律，第一类和第二类的干球温度日变化趋势相近，但其对应的湿球温度日变化规律存在差异。

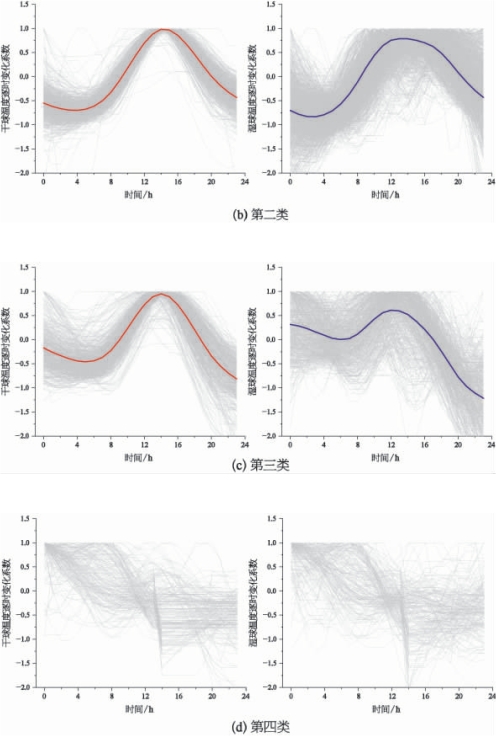
图7.1　武汉地区夏季干、湿球温度逐时变化趋势聚类结果

图7.2　南宁地区夏季干、湿球温度逐时变化趋势聚类结果

由图7.2中可见，南宁地区的干、湿球温度逐时变化趋势可聚成4类，其中第四类无明显变化规律，第一类、第二类和第三类的干球温度日变化趋势均比较相似，但其对应的湿球温度日变化规律存在差异。

由于聚类所采用的系数矩阵以日为单位考虑了干球温度和湿球温度两种气象要素的同时发生性，因此聚类结果中的每一类干、湿球温度日变化趋势均发生在同一天，一定程度上保留了两气象要素的日变化趋势之间的耦合关系，符合客观规律。

基于上述聚类分析，本研究统计得到了武汉和南宁聚类结果中各类的权重占比，结果如图7.3所示。

为保证选取的干、湿球温度的典型逐时变化趋势具有代表性，本研究以聚类结果中权重占比最高的一类作为逐时化系数生成的基础。因此，在武汉和南宁的干、湿球温度聚类结果中，均选择第一类聚类结果。以选择的聚类结果的类质心曲线为基础，即可计算得到对应干球温度和同时发生的湿球温度的逐时化系数。

图7.3　武汉、南宁地区的聚类结果占比

（2）夏季干球温度和同时发生的湿球温度设计日数据的对比分析

以上述计算得到的干球温度和同时发生的湿球温度逐时化系数为基础，结合不同不保证水平的夏季空调室外计算温度，即可生成夏季干球温度和同时发生的湿球温度设计日。

在我国现行的《民用建筑供暖通风与空调设计规范》（GB 50736—2012）中，同样提供了一组夏季空调负荷计算用的干球温度设计日和湿球温度设计日。为了探究本研究设计日与现行规范设计日之间的差别，以同样的基础数据计算得到了武汉和南宁地区的室外不保证50 h的本研究设计日和现行规范设计日，同时从当地的实际气象观测数据中筛选出与设计日极端程度相近的真实日数据，以此进行对比分析，结果如图7.4和7.5所示。

图7.4　武汉地区的本研究设计日和现行规范设计日的对比

图7.5　南宁地区的本研究设计日和现行规范设计日的对比

从图7.4和7.5中可以看出，对于武汉和南宁地区，相比于现行规范设计日，本研究设计日的日变化趋势更接近真实日。尤其对于湿球温度设计日，在现行规范设计日中湿球温度被视为恒定值，这并不符合客观规律，而本研究设计日通过聚类的方法合理地描述了湿球温度的日变化特征，填补了现行规范的空白。

7.2.4.2　冬季供暖干球温度设计日——以沈阳、张家口为例

（1）冬季干球温度的逐时变化趋势的聚类分析

冬季供暖干球温度设计日的构造是以冬季干球温度的典型逐时变化趋势为基础的。为了获取沈阳、张家口地区的冬季干球温度的典型逐时变化趋势，首先从沈阳、张家口地区的30年逐时气象数据中选取每年的12—2月的干球温度数据，以日为单位从干球温度数据中提取对应的逐时变化趋势，然后构建干球温度系数矩阵。以该系数矩阵为基础，采用K-Means聚类方法对沈阳和张家口地区的干球温度逐时变化趋势进行聚类分析，结果如图7.6和7.7所示。

图7.6　沈阳地区冬季干球温度逐时变化趋势聚类结果

由图7.6中可见，沈阳地区的冬季干球温度逐时变化趋势可聚成4类，其中第四类的干球温度变化规律相对杂乱，而其他类中的干球温度日变化特征各不相同。

图7.7　张家口地区冬季干球温度逐时变化趋势聚类结果

由图7.7中可见，张家口地区的冬季干球温度逐时变化趋势可聚成4类，其中第四类的干球温度变化规律相对杂乱，而其他类中的干球温度日变化特征各不相同。

基于上述聚类分析，本研究统计得到了沈阳和张家口聚类结果中各类的权重占比，结果如图7.8所示。

由图7.8中可见，在沈阳和张家口的聚类结果中，第一类的占比均远远高于其他类。因此，对于沈阳和张家口地区，均选择第一类干球温度逐时变化趋势的聚类结果。以选择的聚类结果的类质心曲线为基础，可以计算得到对应干球温度的逐时化系数。

图7.8　沈阳、张家口地区的聚类结果占比

（2）冬季供暖干球温度设计日数据的对比分析

以干球温度逐时化系数为基础，结合不同不保证水平的冬季供暖计算温度，即可生成得到冬季供暖干球温度设计日。

在我国现行的《民用建筑供暖通风与空调设计规范》中，提供了历年平均不保证5 d日平均温度作为冬季供暖室外计算干球温度，以满足连续供热设计中稳态负荷计算的需要。然而，在间歇供暖系统中，需要以冬季供暖的动态负荷计算作为设计基础，现行规范提供的点工况设计值无法满足这一需求，而本研究设计日可以填补这一空白。

为了验证本研究的冬暖供暖干球温度设计日构造的合理性，对比了历年平均不保证5 d的本研究设计日和现行规范设计日（恒定值），以及对应真实日之间的差别，结果如图7.9和图7.10所示。

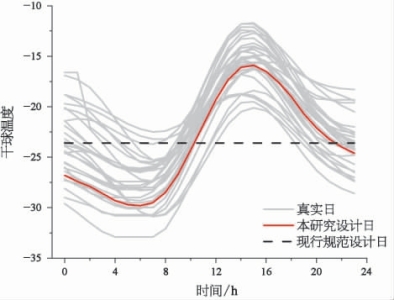
图7.9　沈阳地区的本研究设计日和现行规范设计日的对比

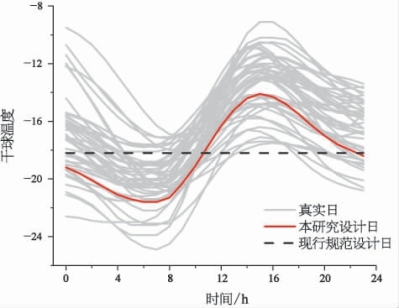
图7.10　张家口地区的本研究设计日和现行规范设计日的对比

从图7.9和图7.10中可以看出，本研究设计日能够较为准确地反映对应真实日的日变化规律。同时，相比于现行规范提供的冬季供暖设计值，本研究提供的设计日数据能够提供更丰富的室外干球温度信息，如日较差、峰谷时刻等，从而能够满足更为精细化的供暖系统设计需求。