6.2.1 数据驱动模型计算方法
6.2.1.1 数据驱动模型介绍
由于很多研究发现PMV模型常与实际情况存在一定误差,因此建立基于数据驱动的供暖空调室内设计参数确定的模型可供选择和参考。基于中国热舒适数据库,将在选择气候区、建筑类型、季节等条件后,得到人体对热环境满意率在80%以上的室内温度设计范围。
数据驱动模型输入参数包括气候区、季节和建筑类型。气候区分为严寒地区、寒冷地区、夏热冬冷地区、夏热冬暖地区和温和地区。季节分为夏季和冬季。建筑类型分为办公建筑和住宅建筑。基于中国室内环境参数数据库,得到筛选后的数据,计算出每一组数据的SET值,进行Logistic回归,得到满意率Y与SET的函数关系式。然后对得到的函数关系式做显著性检验,若P<0.05则通过,若P≥0.05则不通过,需要补充或清洗数据。随后基于满意率的设定条件,一般设定为80%的满意率,得到舒适的SET区间。最后基于所选条件下的代谢率、服装热阻、风速和相对湿度的平均值,计算得到舒适温度区间。
本模型从中国热舒适数据库中筛选数据的规则如下:
(1)仅选择1级和2级数据。
(2)仅选择冬季和夏季数据,不考虑过渡季。
(3)建筑类型仅选择办公建筑和住宅建筑。
(4)建筑需有暖通空调设备并在调研时间开启。
(5)少数民族地区,农村地区暂不考虑。
(6)人体代谢率在1.5 met以下,不考虑高代调率情况。
(7)空气流速在0.5 m/s以下,不考虑高风速情况。
6.2.1.2 标准有效温度SET模型
室内热环境舒适温度范围会受到人体代谢率、服装热阻、相对湿度、风速等参数的影响。例如:如果冬季人的服装热阻较大,则可接受温度下限也会偏低;如果人的服装热阻较小,可接受温度下限会偏高,因此如果仅仅考虑温度一个参数的影响可能会造成误差。标准有效温度SET则综合考虑了人体代谢率、服装热阻、空气温度、平均辐射温度、相对湿度及风速6个参数的综合影响。SET模型是由Gagge基于人体对热环境的生理调节模型二节点模型建立,被收录于ASHRAE Standard 55 2017。在实际研究中发现SET模型与平均皮肤温度、皮肤湿润度等生理指标有很好的相关性,并且可以有效预测人体主观热感觉。由于数据驱动模型中使用了标准有效温度SET指标,在此对SET进行介绍。
二节点模型是SET计算的基础。二节点模型把人体设置为核心层和皮肤层两个集中热层,是一种简化的集总参数模型。人体的核心层新陈代谢,产生出热量,如果在环境较冷的情况下,冷颤反应可产生额外的热量。大部分的热量通过皮肤表面通过显热与潜热换热散失到环境中,其中小部分热量通过呼吸散热散失到环境中,小部分热量蓄积在人体。二节点模型如图6.2所示。
二节点模型热平衡方程如下:
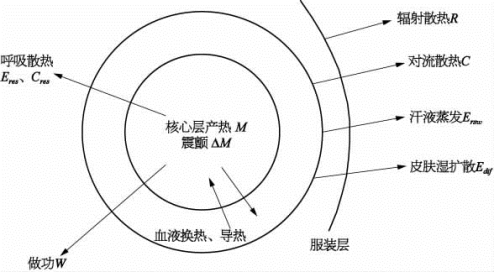
图6.2 二节点模型图示
核心层:
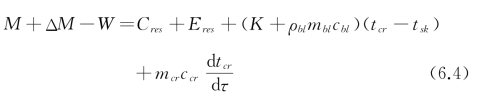
皮肤层:
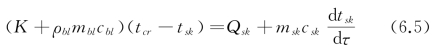
式中 M,ΔM——人体代谢率与冷颤增加的代谢率,W/m2;
W——人体对外做功,W/m2;
Cres,Eres——呼吸显热与呼吸潜热散热量,W/m2;
ρbl——血液密度,kg/L;
mbl——皮肤层血流量,L/(m2·s);
cbl,ccr,csk——血液,核心层与皮肤层的比热容,J/(kg·K);
tcr——人体核心层温度,℃;
mcr,msk——皮肤层与核心层的质量,kg;
τ——时间,s;
Qsk——皮肤散热量,W/m2。
二节点模型可以计算出平均皮肤表面温度、皮肤湿润度、皮肤散热量等参数,为计算SET指标提供基础。SET的计算程序参考ASHRAE Standard 55—2017。本方法将首先计算得到SET的舒适区间,再基于当前条件下的平均参数值计算得到舒适温度区间。
6.2.1.3 Logistic回归方法
在实际调研数据中,人体满意率不一定随SET呈现规律性变化,因此需要找到满意率随SET变化的整体趋势,也有可能会由于数据的缺少难以找到80%满意率的边界,需要基于已有数据的情况对边界进行预测。Logistic回归用于预测某一件事情发生的概率,在医学、经济领域有广泛应用,在热舒适领域也有一定程度的应用。本模型使用了无序多分类Logistic回归,用于对舒适区间的回归和预测。在本模型设定TSV<-1.5为冷不舒适,-1.5≤TSV≤1.5为舒适,TSV>1.5为热不舒适。其概率分别为P1、Y、P2,处理方法如图6.13所示。
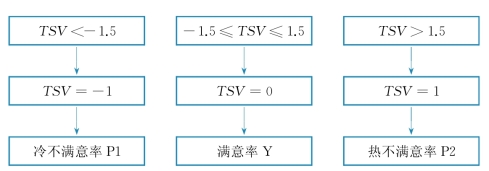
图6.3 热感觉投票处理方法
通过Logistic回归计算,得到如下方程组:

联立得到热舒适率Y随SET变化的函数Y=F(SET),公式如下:
![]()
式中 a1、b1、a2和b2是通过Logistic回归计算得到的参数。
6.2.2 数据驱动模型计算结果
基于中国热舒适数据库筛选后的数据,利用本模型对不同条件的舒适区间进行计算。中国5个气候区分别为严寒地区、寒冷地区、夏热冬冷地区、夏热冬暖地区和温和地区。其中严寒地区夏季短促而凉爽,基本不需供冷,因此暂不分析夏季的情况。夏热冬暖地区最冷月平均温度大于10℃,冬季很少有供暖需求,因此暂不分析冬季情况。温和地区最冷月平均温度满足0~13℃,最热月平均温度满足18~25℃,冬暖夏凉,建筑多为自由运行状态,因此暂时不分析温和地区的情况。本模型中夏季等同于供冷季,冬季等同于供暖季。下面将计算结果分别阐述。
6.2.2.1 严寒地区(https://www.xing528.com)
图6.4为严寒地区冬季的办公建筑和住宅建筑基于Logistic回归得到的人体80%满意率下的SET范围,分别为20.4~25.3℃和20.3~26.4℃。将模型预测结果与实际数据进行对比,可以看出模型预测值与实际数据相符合。本模型除了能预测80%满意率的边界值,也可以有效预测任意具体条件下的人体满意率。
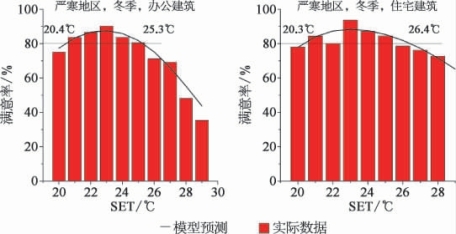
图6.4 严寒地区计算结果
表6.2为Logistic拟合的具体信息,可以看出回归模型显著性较高,具有统计学意义。
表6.2 严寒地区Logistic回归计算结果

表6.3为各个条件下人体代谢率、服装热阻、相对湿度与风速参数的平均值。
基于SET范围和参数的平均值,计算得到80%满意率的温度范围,如表6.4所示。这里的80%满意率指取具体条件下参数平均值,以冬季的办公建筑为例,即假定人体代谢率1 met、服装热阻1.01 clo、相对湿度27%、风速0.07m/s的情况下,预计有80%的人对热环境满意的温度范围。可以看出,住宅建筑舒适区间比办公建筑稍宽。
表6.3 不同条件下参数平均值
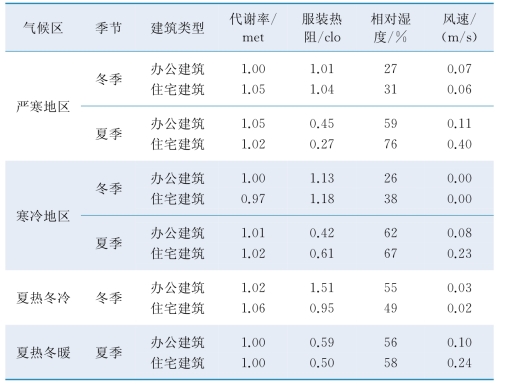
表6.4 严寒地区舒适温度区间

6.2.2.2 寒冷地区
图6.5为寒冷地区冬夏季及办公建筑、住宅建筑基于Logistic回归方法得到的SET范围,与实际数据进行对比,符合良好。
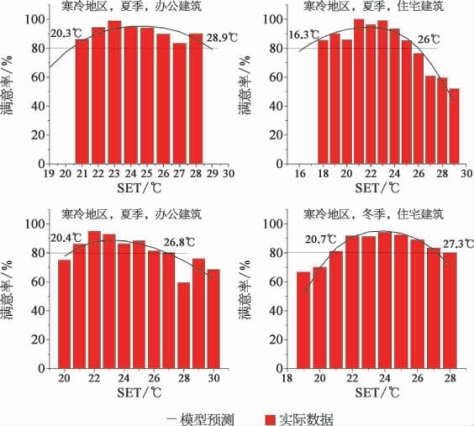
图6.5 寒冷地区计算结果
表6.5为寒冷地区回归模型拟合的信息,可以看出各个情况的回归均有统计学意义。
表6.5 寒冷地区Logistic回归计算结果

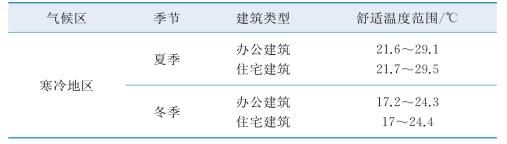
基于SET舒适范围和当前条件代谢率、相对湿度、风速和服装热阻参数的平均值,得到舒适温度区间,见表6.6。
表6.6 寒冷地区舒适温度区间
6.2.2.3 夏热冬冷地区
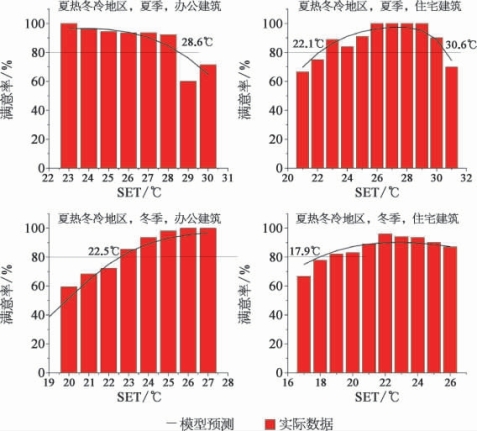
图6.6 夏热冬冷地区计算结果
图6.6为夏热冬冷地区冬夏季及办公建筑、住宅建筑基于Logistic回归方法得到的SET范围,并与实际数据进行对比,有较好的符合度。
表6.7为夏热冬冷地区Logistic回归模型拟合的信息。
表6.7 夏热冬冷地区Logistic回归计算结果

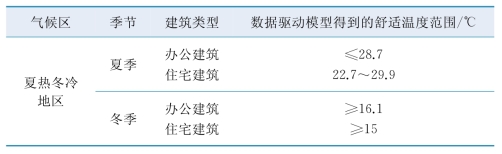
表6.8为夏热冬冷地区舒适温度区间,与严寒地区、寒冷地区相比,夏热冬冷地区的冬季的可接受温度下限要更低,原因可能是常年以来由于夏热冬冷地区冬季没有集中供暖,因此人群对低温有更强的适应性。
表6.8 夏热冬冷地区舒适温度区间
6.2.2.4 夏热冬暖地区
图6.7为夏热冬暖地区夏季办公建筑基于Logistic回归方法得到的SET范围,并与实际数据进行对比,符合性度良好。
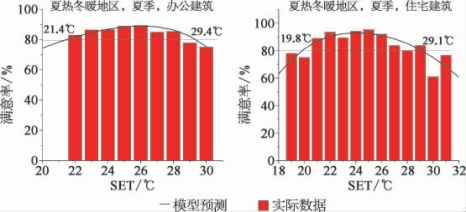
图6.7 夏热冬暖地区计算结果
夏热冬暖地区冬季较短,一般不需供热,因此暂不考虑冬季情况。表6.9为夏热冬暖地区Logistic回归模型拟合的信息,可见显著性较高,模型具有统计学意义。
表6.9 夏热冬暖地区Logistic回归计算结果

再将SET折合成温度。表6.10为夏热冬暖地区舒适温度区间。
表6.10 夏热冬暖地区舒适温度区间

由于数据量的限制,目前得到的各参数值或范围还有待进一步完善。随着数据库的不断扩充,用数据驱动方法计算得到的参数范围将会更趋近于实际情况。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




