平行坐标面圆的轴测投影

在平行投影中,当圆所在的平面平行于投影面时,其投影仍是圆,当圆所在平面倾斜于投影面时,其投影是椭圆。

1.四心法作圆的正等轴测图

平行于某一基本投影面的圆的正等轴测投影常用四心法（四段圆弧连接的近似椭圆）画出。如图4-6所示的是水平圆的正等轴测投影的近似画法,可用同样的方法作出正平圆和侧平圆的正等轴测投影,如图4-7所示。

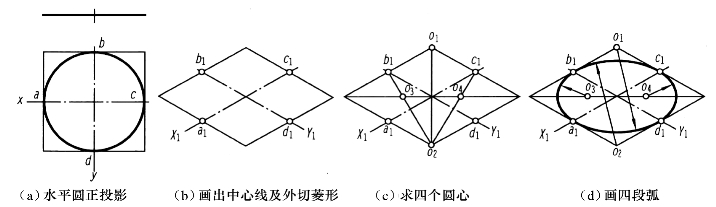
图4-6　水平圆的正等测投影近似画法

(www.xing528.com)

图4-7　正平圆和侧平圆的正等测投影

2.八点法作圆的轴测图

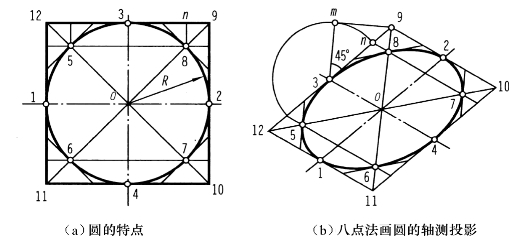
图4-8　八点法作圆的轴测图

圆的轴测投影还可用如图4-8所示的八点法绘出。这种方法适用于任一类型的轴测投影作图时,先作出圆的外切正方形的轴测投影,然后再画圆。为了作出椭圆,先了解依据椭圆的共轭直径用八点法绘制椭圆的原理,如图4-8所示,左图分析了圆上的八个点及其外切正方形平面的特点,右图是该平面连同圆的某一投影,可以看出,圆O的一对相互垂直的直径12和34,在轴测投影中不再相互垂直,这一对直径称为椭圆的共轭直径。5、6、7、8是位于外切正方形对角线上的点,只要在平行四边形对角线上确定5、6、7、8,则可通过连接1、6、4、7、2、8、3、5八个点,较准确地画出椭圆。左图中,△o39是一等腰直角三角形,o33＝39＝o8,而o9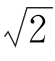＝R,作8n∥34,则3n∶39＝o8∶o9＝1∶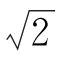。根据平行投影的定比性,在投影图中只要按比例求出点5、6、7、8即可。