平面与平面平行的几何条件及作图方法-土木工程制图

两平面相平行的几何条件是：如果一平面上的一对相交直线,分别与另一平面上的一对相交直线互相平行,则两平面互相平行。利用这个几何条件可以进行平面与平面平行的检验和作图。

【例2-19】　如图2-58（a）所示,已知两平面△ABC和△DEF以及点P的两面投影。

（1）检验两平面△ABC和△DEF是否互相平行?

（2）过点P作一平面平行于△DEF。

解　（1）检验两平面是否平行,只要在一平面上作出两相交直线,检验是否与另一平面上的相交直线平行即可,作图过程如图2-58（b）所示：

1）在△DEF的DF边上找一点G,标出其两面投影g、g′。

2）过g′作g′1′∥a′c′,与d′e′交得1′。

3）过g′作g′2′∥b′c′,与d′e′交得2′。

4）过1′、2′分别作OX轴的垂线,与de交得1、2,连接g1和g2。

5）检验g2是否平行于bc,g1是否平行于ac。本题经检验g2∥bc,g1∥ac,即GⅡ∥BC,GⅠ∥AC,故△ABC∥△DEF。

若检验结果为g2不平行于bc或g1不平行于ac,即可判断△ABC与△DEF一定不平行。(https://www.xing528.com)

（2）过点P作一个平面与△DEF相平行,只要过点P作出两条与△DEF平行的相交直即可。作图过程如图2-58（b）所示：

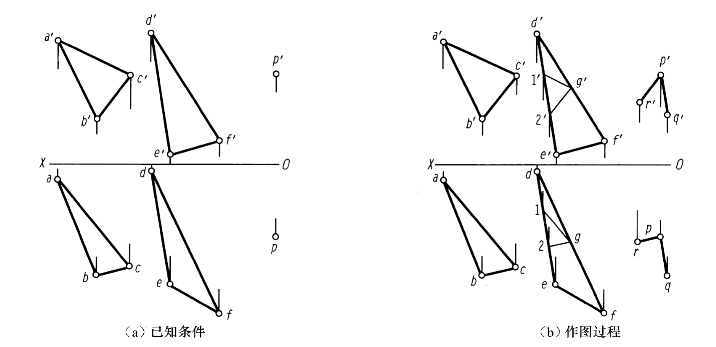
图2-58　半面与半面半行的检验和作图

1）过p′作p′r′∥g′2′,p′q′∥d′e′。

2）过p作pr∥g2,pq∥de。

3）因两条相交直线即可确定一个平面,故pqr和p′q′r′即为所求平面的两面投影。

图2-59　特殊位置的两平面平行

在特殊情况下,当两平面都是同一投影面的垂直面时,则两平面的平行关系可直接在两平行平面有积聚性的投影中反映出来,即两平面的有积聚性的同面投影互相平行。如图2-59（a）所示,设铅垂面P和Q在空间互相平行,故它们的H面投影PH∥QH,P和Q两面投影图的表示方式如图2-59（b）所示；反之,因H面中的积聚投影PH∥QH,由之所作的H面垂直面P和Q在空间亦必互相平行。