直线与平面垂直的几何条件是:只要直线垂直于该平面上的任意两条相交直线,不管该直线是否通过两条相交直线的交点,则直线与平面必相互垂直。
1.一般位置的直线与平面垂直
在前面的学习中已经知道,两直线垂直,当其中一条直线为投影面的平行线时,则两直线在该投影面上的投影仍相互垂直。因此在投影图上作平面的垂线时,可首先作出平面上的一条正平线和一条水平线作为平面上的相交两直线,再作垂线。此时所作垂线与正平线所夹的直角,其V面投影仍是直角,垂线与水平线所夹的直角,其H面投影也是直角。
【例2-16】 如图2-54(a)所示,已知空间一点M和平面ABCD的两面投影,求作过M点与平面ABCD相垂直的垂线MN的投影(MN可为任意长度)。
解 作图过程如图2-54(b)所示:
(1)过a′作a′1′∥OX轴,与b′c′交得1′,过1′作OX轴的垂线,与bc交得1,连接a1并延长a1,过m作a1的垂线。
(2)过a作a2∥OX轴,交bc得2,过2作OX轴的垂线,交b′c′得2′。
(3)连a′2′并延长a′2′,过m′作a′2′的垂线m′n′。
(4)过n′作OX轴的垂线,得n点,将m′n′和mn画成粗实线。m′n′、mn即为所求垂线MN的投影。
本题只是要求作出一条任意长度的垂线MN,故在取N点的投影时,可在两面投影中的垂线上任意定出点N,只是要求点N的两面投影符合投影规律而已。
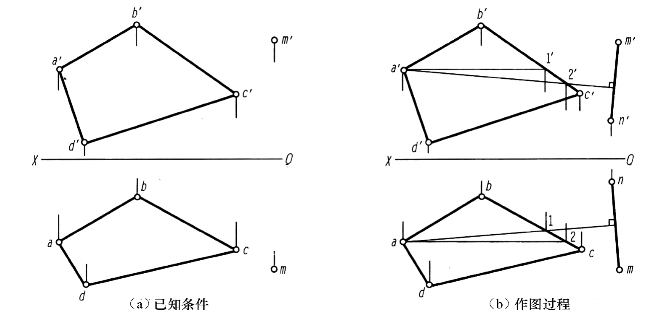
图2-54 一般位置的直线与平面垂直
2.特殊位置的直线与平面垂直
特殊位置的直线与平面相垂直,只有如图2-55所示的两种情况。
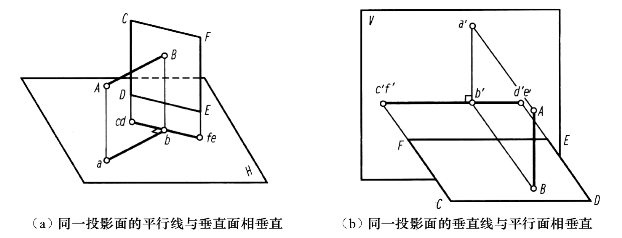
图2-55 特殊位置的直线与平面垂直的投影特性
如图2-55(a)所示是同一投影面的平行线与垂直面相垂直的情况,图中AB是水平线,CDEF是铅垂面,由立体几何可推知:与水平线相垂直的平面,一定是铅垂面;与铅垂面相垂直的直线,一定是水平线;而且水平线的H面投影,一定垂直于铅垂面的有积聚性的H面投影,即图中ab⊥cdef。同理,正平线与正垂面相垂直,侧平线与侧垂面相垂直,也都属于这种情况。
综合上段所述,可以得出结论:与投影面平行线相垂直的平面,一定是该投影面的垂直面;与投影面垂直面相垂直的直线,一定是该投影面的平行线;投影面平行线在所平行的投影面上的投影,必垂直于该投影面垂直面的有积聚性的同面投影。
如图2-55(b)所示是同一投影面的垂直线与平行面相垂直的情况,图中AB是铅垂线,CDEF是水平面,由立体几何可推知:与铅垂线相垂直的平面,一定是水平面;与水平面相垂直的直线,一定是铅垂线;而且铅垂线的V面投影,一定垂直于水平面的有积聚性的V面投影,即图中a′b′⊥c′d′e′f′。同理,正垂线与正平面相垂直,侧垂线与侧平面相垂直,也都属于这种情况。
综合上段所述,可以得出结论:与投影面垂直线相垂直的平面,一定是该投影面的平行面;与投影面平行面相垂直的直线,一定是该投影面的垂直线;投影面垂直线的投影必定与平面的有积聚性的同面投影相垂直。(https://www.xing528.com)
【例2-17】 如图2-56(a)所示,已知点A和直线BC的两面投影,求点A与直线BC间的真实距离。
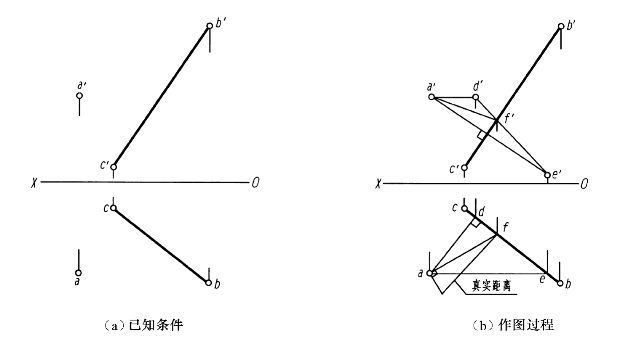
图2-56 求点到直线的距离
解 (1)分析:求点A到直线BC的真实距离,只要作出点A到直线BC的垂线AF,然后求出点A与垂足F的真实距离即可。为此,可以先过A点作一平面与直线BC垂直,求出平面与直线BC的交点F,连接AF,则AF一定垂直于BC,最后用直角三角形法求出AF的真实长度。
(2)作图过程如图2-56(b)所示:
1)过a作ab⊥bc,与bc交得d,过d作OX轴的垂线,交过a′且与OX轴平行的直线于d′;过a作ae∥OX轴,与bc交得e,过e作OX轴的垂线,交过a′且与b′c′垂直的直线于e′,连接d′e′。
2)求出直线BC与平面△ADE的交点F的两面投影f、f′,连接af、a′f′。
3)因所作的△ADE⊥BC,又AF在△ADE上,故AF⊥BC,F为垂足。
4)利用直角三角形法求出AF的真实长度,标注在投影图上。
【例2-18】 如图2-57(a)所示,求作一直线MN与两交叉直线AB和CD相交,且与另一直线EF平行。
解 (1)分析:过直线AB若作出一个平面与EF平行,则在这个平面上可以有无数条直线与EF平行,且与AB相交。要满足所求直线与直线CD也相交,只需求出直线CD与所作平面的交点M,过M作MN∥EF,与AB交于N点即可。
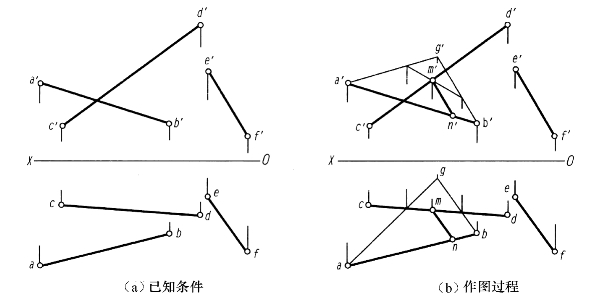
图2-57 作直线与交叉两直线相交且与已知直线平行
(2)作图过程如图2-57(b)所示:
1)过b′作b′g′∥e′f′,过b作bg∥ef。
2)求出直线CD与平面ABG的交点M的投影m、m′
3)过m′作m′n′∥e′f′,与a′b′交得n′
4)过m作mn∥ef,与ab交得n或过n′作OX轴的垂线,与ab交得n,结果一样。
5)完成作图,mn、m′n′即为所求。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




