直角三角形法求直线实长及倾角

从前面直线的投影可以看出,对于特殊位置直线,比较容易从投影求得它们的实长和倾角,但对于一般位置直线,直接从其三面投影中很难求出实长和倾角。但可以采用直角三角形法求线段的实长和倾角,即在投影、倾角、实长三者之间建立起直角三角形关系,从而在直角三角形中求出实长和倾角。

根据几何学原理可知：直线与其投影面的夹角就是直线与它在该投影面的投影所成的角。如图2-29（a）所示,求直线AB与H面的夹角α及实长,我们可以自A点引AB1∥ab,得直角三角形AB1B,其中AB是斜边,∠B1AB就是α角,直角边AB1＝ab,另一直角边BB1等于B点的Z坐标与A点的Z坐标之差,即BB1＝zB－zA＝Δz。所以在投影图中就可根据线段的H投影ab及坐标差Δz作出与△AB1B全等的一个直角三角形,从而求出AB与H面的夹角α及AB线段的实长,如图2-29（b）所示。

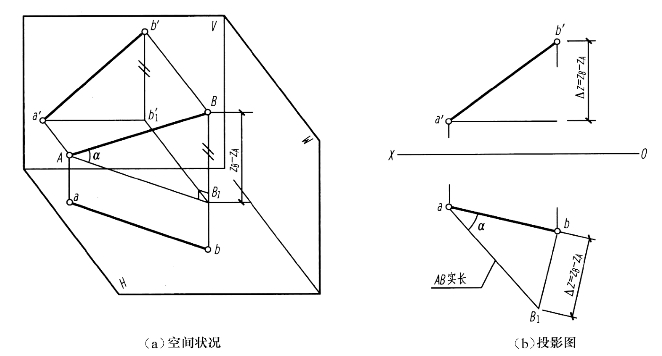
图2-29　直角三角形法求线段实长及倾角α

由此,我们总结出AB的投影、倾角与实长之间的直角三角形边角关系如表2-3所示。

表2-3　线段AB的直角三角形边角关系

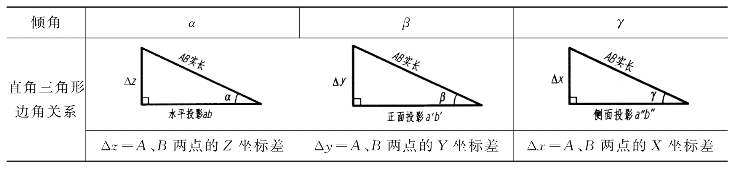
从表2-3可以看出,构成各直角三角形共有四个要素,即：①某投影的长度（直角边）；②坐标差（直角边）；③实长（斜边）；④对投影面的倾角（投影与实长的夹角）。在这四个要素中,只要知道其中任意两个要素,就可求出其他两个要素。并且我们还能够知道：不论用哪个直角三角形,所作出的直角三角形的斜边一定是线段的实长,斜边与投影的夹角。就是该线段与相应的投影面的倾角。

利用直角三角形关系图解关于直线段投影、倾角、实长问题的方法称为直角三角形法。在图解过程中,若不影响图形清晰时,直角三角形可直接画在投影图上,也可画在图纸的任何空白地方。(www.xing528.com)

【例2-5】　如图2-30（a）所示,已知直线AB的水平投影ab和A点的正面投影a′,并知AB对H面的倾角α＝30°,B点高于A点,求AB的正面投影a′b′。

解　（1）分析：在构成直角三角形四个要素中,已知其中两要素,即水平投影ab及倾角α＝30°,可直接作出直角三角形,从而求出b′。

（2）作图步骤：

1）在图纸的空白地方,如图2-30（c）所示,以ab为一直角边,过a作30°的斜线,此斜线与过b点的垂线交于B0点,bB0即为另一直角边Δz。

2）利用bB0即可确定b′,连接a′b′即得AB得正面投影,如图2-30（b）所示。

此题也可将直角三角形直接画在投影图上,以便节约时间与图纸,如图2-30（b）所示。

图2-30　利用直角三角形法求a′b′