土木工程制图：三面投影体系及其应用

1.点的三面投影形成

图2-17（a）是空间点A的三面投影的直观图,过A点分别向H、V、W面的投影为a、a′、a″。

将三面投影体系按投影面规律展开,便得到A点的三面投影图,因为投影面的大小不受限制,所以通常不必画出投影面的边框。图2-17（b）是点A的三面投影图。

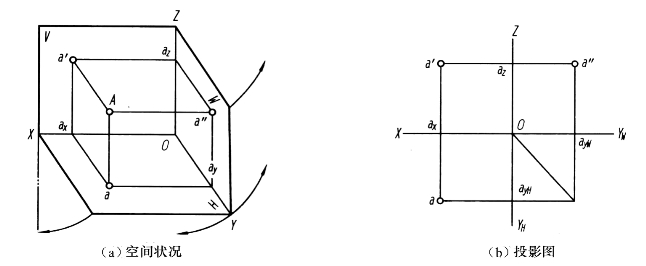
图2-17　点的三面投影

2.点的三面投影规律

从图2-17（a）可看出：aax＝Aa′＝a″ax,即A点的水平投影a到OX轴的距离等于A点的侧面投影a″到OZ轴的距离,都等于A点到V面的距离。由图2-17（a）还可看出,由Aa′和Aa确定的平面Aaaxa′为一矩形,故得aax＝Aa′（A点到V面的距离）,a′ax＝Aa（A点到H面的距离）。

同时,还可以看出：因Aa⊥H面,Aa′⊥V面,故平面Aaaxa′⊥H面,Aaaxa′⊥V面,则OX⊥a′ax,OX⊥aax。当两投影面体系按展开规律展开后,aax与OX轴的垂直关系不变,故a′axa为一条垂直于OX轴的直线,即a′axa⊥OX。

同理可知：a′a″⊥OY,见图2-17（b）。

综上所述,可得点的三面投影规律如下：

（1）一点的水平投影与正面投影的连线垂直于OX轴；

（2）一点的正面投影与侧面投影的连线垂直于OZ轴；

（3）一点的水平投影到OX轴的距离等于该点的侧面投影到OZ轴的距离,都反映该点到V面的距离。

由上述规律可知,已知点的两个投影便可求出第三个投影。

3.例题分析

下面用例题说明如何根据点的两个投影求出第三个投影。

【例2-1】　如图2-18（a）所示,已知点A、B的两面投影求作第三面投影。

图2-18　已知两面投影求第三面投影

解　（1）分析：由三面投影规律可知,一点的水平投影与正面投影的连线垂直于OX轴；一点的正面投影与侧面投影的连线垂直于OZ轴；一点的水平投影到OX轴的距离等于该点的侧面投影到OZ轴的距离,都反映该点到V面的距离。(www.xing528.com)

（2）作图：过程如图2-18（b）所示。

1）过O向右下角作45°辅助线,过a′作a′a″⊥OZ轴,过a作直线平行于OX轴,与45°辅助线相交后作平行于OZ轴的直线且交a′a″于a″。

2）过b′作bb′⊥OX轴,过b″作直线平行OZ轴,与45°辅助线相交后作平行于OX轴的直线交bb′于b。

4.投影面上的点和投影轴上的点

如果空间点处于特殊位置,比如点恰巧在投影面上或投影轴上,那么这些点的投影规律又如何呢?如图2-19所示。

图2-19　投影面、投影轴上的点的投影

（1）若点在投影面上,则点在该投影面上的投影与空间点重合,另两个投影均在投影轴上,如图2-19所示中的点A和点B；

（2）若点在投影轴上,则点的两个投影与空间点重合,另一个投影在投影轴原点,如图2-19所示中的点C。

5.点的投影与坐标的关系

空间点的位置除了用投影表示以外,还可以用坐标来表示。

可以把投影面当作坐标面,把投影轴当作坐标轴,把投影原点当作坐标原点,则点到三个投影面的距离便可用点的三个坐标来表示（如图2-20所示）,点的投影与坐标的关系如下：

图2-20　点的投影与坐标

A点到H面的距离Aa＝Oaz＝a′ax＝a″ay＝z坐标；

A点到V面的距离Aa′＝Oay＝aax＝a″az＝y坐标；

A点到W面的距离Aa″＝Oax＝a′az＝aay＝x坐标。

由此可见,已知点的三面投影就能确定该点的三个坐标；反之,已知点的三个坐标,就能确定该点的三面投影或空间点的位置。