为了帮助读者学习执行机构的动特性,这里稍微介绍一下直流电动机的数学模型。对于不想了解电动机特性原理的读者可跳过这一节。
电动机的数学模型可以看成由两部分组成:电气部分和机械部分。对于电气部分,是一个典型的电感(L)、电容(C)和电阻(R)串联的电路,由外加电压(u)形成电流(i),输出转矩,这可用微积分方程描述如下:
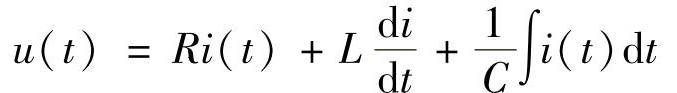
式中,u(t)是外加电压和电动机反电动势的组合电压。机械部分是一个典型的质量(m)、弹簧(k)和阻尼(c)组合的系统,外加作用力矩(T),形成旋转角位移(θ)。可用微积分方程描述如下:
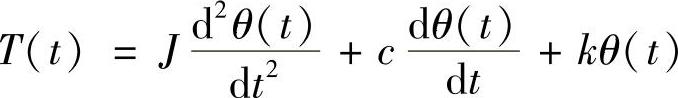
式中,T是施加到这个机构的外转矩,这里是电动机电磁转矩、负载转矩和哥伦布摩擦转矩的合成转矩;J为系统转动惯量(1/2Mr2);θ为角位移;k为弹性系数;c为阻尼系数。为了便于研究,假设绕组间的容抗C为零,并假设电枢和轴是刚性的,那么一个直流有刷电动机可以用图11-4来等效。
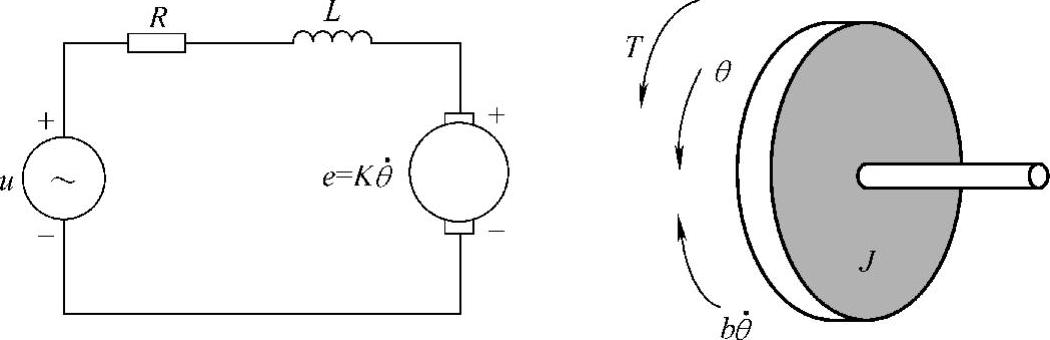
图11-4 直流电动机等效模型
为了建立一个量的概念,可假设:
电枢转动惯量:J=0.01kgm2/s2
机械阻尼系数:c=0.1N·m
电动势常数:K=Ke=Kt=0.01N·m/A
电阻:R=1Ω
绕组电感:L=0.5H
输入电压:u=电压源
输出角度θ=轴位移角度
另外,电动机转矩(T)是电枢电流的函数,反电势(e)是电动机转速的函数:
T=kti
e=kedθ/dt
从图11-4可得
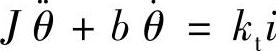
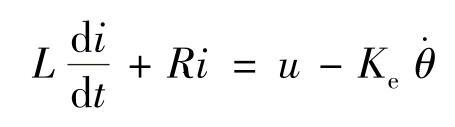
通过拉普拉斯变换,上式可表达为
(JS+b)θ(S)=ktI(S)
(LS+R)I(S)=u(S)-keθ(S)(https://www.xing528.com)
代换上两式中的电流,上式又可表示为角位移为输出和电压为输入的开环传递函数,即
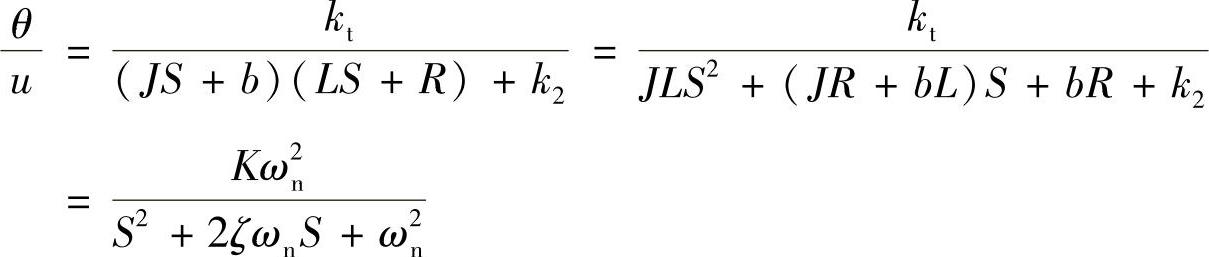
上式是一个典型的二阶系统在频率域的数学模型。其中ζ是系统阻尼系数,ωn是系统欠阻尼自然振荡频率。当ζ=0时,系统不收敛振荡,是一个不稳定系统。当0<ζ<1时,系统衰减振荡。当ζ≥1时,系统过阻尼,系统不会超调更不会振荡。闭环控制系统可以改变一个系统的阻尼系数和自然振荡频率,使其满足应用中需要的稳定性和快速性要求。
一个电动机在物理上包含有两个主要储能器件:电感线圈和转动惯量。如果将弹性和容抗都加入到模型中,那么传递函数就会变为一个四阶的线性常微分方程系统,再加上通常使用的PID闭环控制器,又会增加系统的阶数。所以,在实际应用中,真正为二阶或一阶的系统极少。由于对高阶系统求解相对复杂一些,加之所有高阶系统可以分解为二阶或一阶系统的串联物,对在系统中起主要作用的二阶子系统先进行分析可以帮助简化系统,加深对系统的理解,也利于调试。
对于一个稳定的二阶系统,它的好坏可通过时域阶跃输入的反应特性来衡量,即从输出的超调、延时、上升时间、稳定时间和稳定误差五个方面进行描述,也可从S域或Z域系统根和零点的位置描述系统的稳定特性。
对于前面所述的二阶电动机系统,角位移为输出,电压为输入:
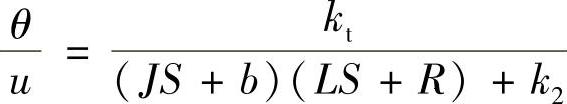
将该方程输入Matlab的分子、分母机构内,为
num=K1
den=(Js+b)(Ls+R)+K2
并用Matlab的M文档方式定义所有变量值,比如:
J=0.01;b=0.1;K1=100;K2=0.01;R=1;L=0.5;num=K1;
den={(J∗L)[(J∗R)+(L∗b)][(b∗R)+K2]};
title(‘Step Response for the Open Loop System’)
为了观察这个开环系统的性能,可在上述Matlab M文档内加上如下指令:
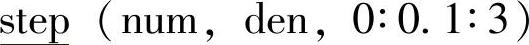
然后在指令框内运行该M文档,就可得到图11-5。
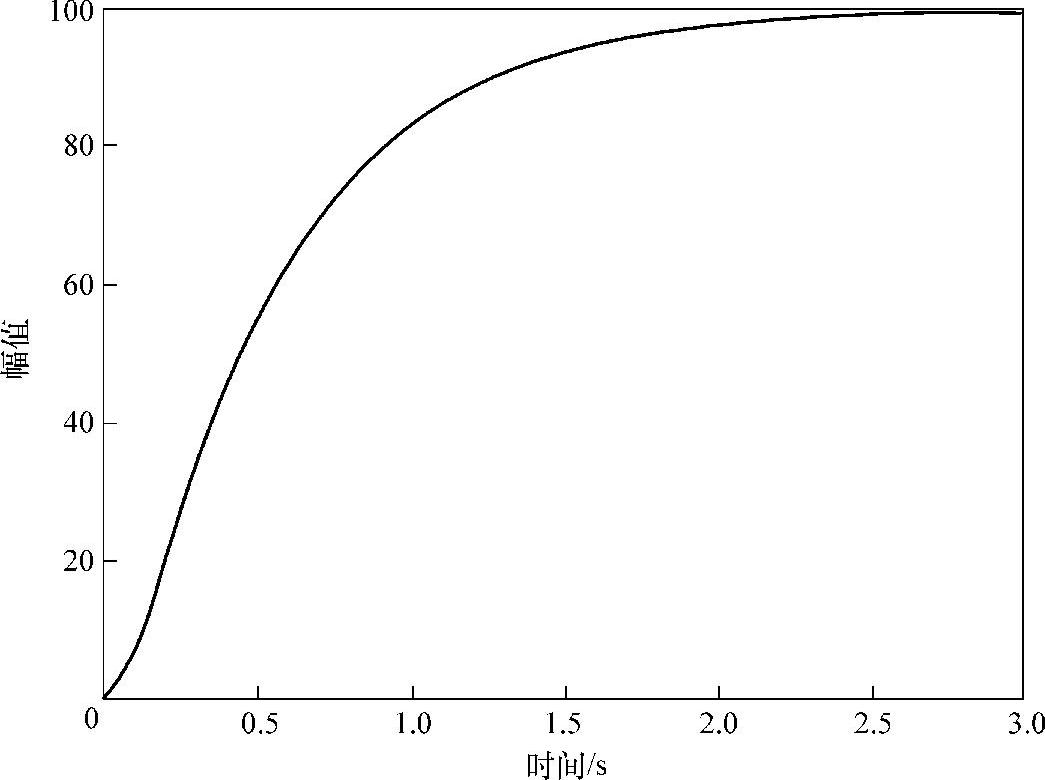
图11-5 电动机开环系统阶跃响应
从图11-5可看到,电动机花了3s才到达稳定值。对于AMT来讲,虽然系统不振荡很稳定,但这样的反应速度显然太慢,形成合适的闭环反馈后就可以加快速度。
如用状态方程描述,可以转角和电流作为状态量,那么:
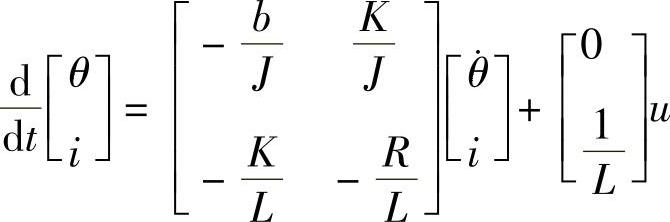
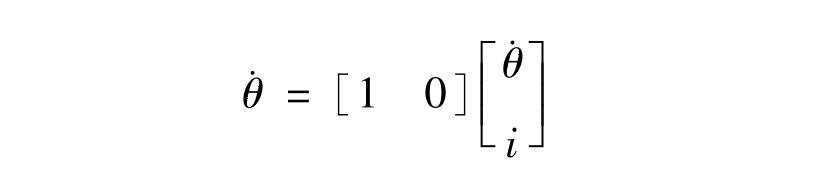
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




