本章简化计算方法-钢板-砖砌体组合加固改造技术试验研究与应用

1）极限状态及基本假定

根据前面的试验现象与分析可知，钢板-砖砌体组合梁的破坏始于组合梁剪跨段钢板的局部屈曲，钢板屈曲发生后变形快速增大，达到峰值荷载后，试件承载力下降。此外，试件从钢板发生局部屈曲到达峰值荷载一般只有1～2个加载等级。因此，可以将弯矩、剪力复合作用下钢板局部屈曲的产生作为试件的极限状态，而此时的荷载作为试件的抗剪承载力。

本节在推导钢板-砖砌体组合梁的抗剪承载力时用到以下假定：

（1）截面的平均应变满足平截面假定；

（2）组合梁截面上的剪力全部由U形外包钢板的腹板承担；

（3）钢板的应力-应变关系采用线弹性模型；

（4）极限状态时忽略控制截面上砌体部分的压应力。

根据试验现象可知，当钢板开始发生局部屈曲时，组合梁上砖砌体部分已经沿加载点至支座连线整体断裂掉，断裂部分相对组合梁发生了较大程度的错动，砌体部分退出了共同工作，因此可以忽略控制截面上砌体部分的压应力。(www.xing528.com)

2）抗剪承载力

根据文献[57]的理论分析与推导，得到钢板-砖砌体组合梁在弯矩、剪力共同作用下剪跨段钢板发生局部屈曲时的抗剪承载力简化计算公式为

式（7-4）中，P为钢板-砖砌体组合梁的抗剪承载力（kN）；L为组合梁剪跨段长度（mm）；a为剪跨段对拉螺栓的水平间距（mm）；t为组合梁中侧板的厚度（mm）；h为组合梁中钢腹板的高度（mm）；I为组合梁中U形截面的惯性矩（mm4）；y为U形截面中和轴以上高度（mm）；σcr为不均匀正应力作用下钢板的临界屈曲应力，按公式（7-5）进行计算；τcr为纯剪应力作用下钢板的临界屈曲应力，按公式（7-6）进行计算；K为对螺栓布置影响系数，按公式（7-7）进行计算；γ为修正系数，取值为0.95。

在公式（7-4）～公式（7-7）中，E为钢材的弹性模量（MPa）；μ为钢材的泊松比，此处取值为0.3；c为组合梁的中和轴高度（mm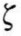）；为没有量纲的变量，它是组合梁中局部屈曲侧板和底部约束板尺寸的函数，称之为约束系数，其由文献[58]中关于槽形截面的外伸翼缘类的公式（7-8-4）确定；tc为组合梁底部钢板的厚度（mm）；b为组合梁底部钢板的宽度（mm）。

根据公式（7-3）～公式（7-7）计算得到钢板-砖砌体组合梁的抗剪承载力见表7-6所示，表中试验值为剪跨段侧板发生局部屈曲时荷载值的1/2。由表7-6可知，本章给出的抗剪承载力计算值与试验值总体上比较接近。因此，该简化计算方法可以作为钢板-砖砌体组合梁在工程应用中的抗剪承载力设计提供参考。

表7-6 理论计算值与试验值比较结果