土力学新论：图17.12和17.13统一强度理论与准则的关系

中文的美与英文的beauty同义但又有所不同。按照英文的定义，“The beauty is a combination of qualities that give pleasure to the senses or lift up the mind，spirit or the intellect”。Beauty不但包括视觉、听觉和是非感的美感，还包括对人的思想、心灵和智力的提升。

有大量的文献讨论过科学的美、数学和物理的美。菲尔兹奖（相当于数学中的诺贝尔奖）获得者丘成桐教授说“数学家找寻美的境界，讲求简单的定律，解决实际问题”。著名数学家普恩卡勒也认为：“数学家非常重视他们的方法是否优美，这并非华而不实。到底是什么使我们感觉到一个解答，一个证明的优美呢？那就是各个部分之间和谐、对称以及恰到好处的平衡。一句话，那就是井然有序，统一协调，从而使我们对整体以及细节都能有清楚的认识和理解。这正是产生伟大结果的地方。”世界著名数学大师陈省身经常告诉大家：“数学就应该是简单美丽的。”数学家把数学的美作为数学研究的最高境界。

也有学者讨论强度理论的美。Prager和Hodge以及Paul认为Huber-von Mises准则的美在于它的数学的简单，澳大利亚Griffith大学教授称“统一强度理论是超越其他各种破坏准则的”，新加坡南洋理工大学教授[63]称“双剪统一强度理论的美在于它的合理性”。

Tzanakis等[64]总结了科学美的六要素，分别是：①概念的清晰性：在建立和发展一个理论时的清晰的；②简约性：文雅和经济的推理；③统一性：先前相互无关的概念、方法、理论或现象的统一；④自然性；⑤对称性；⑥类比性。2004年是第四强度理论提出100年（Huber 1904），在第四强度理论诞生地——世界历史文化名城克拉科夫召开了纪念Huber准则100年的国际会议，俞茂宏应邀作了“强度理论的美”的大会特邀闭幕报告，报告中讨论了Huber准则的美和统一强度理论的美。

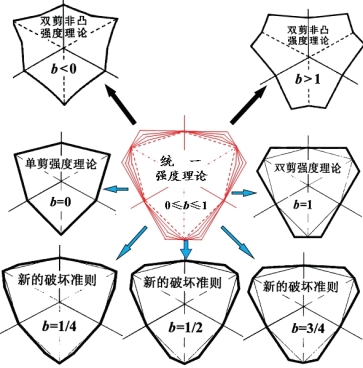
统一强度理论的美表现在很多方面。它的力学模型具有清晰的概念，对称均衡；它的数学表达式具有简约之美；它是从最基本的力学模型推导得出，而不是方程的拟合，具有自然之美；它的极限线具有对称之美；它的变化无穷性使它具有功能强大之美；它的极限线覆盖了域内所有的范围（图17.12），并将己有的一些著名强度理论作为特例或线性逼近而包含于其中，将一些相互无关的强度理论统一于一体，它又具有统一之美。它的工程应用可更好地发挥材料和结构的强度潜力达16%～33%，因此，它还具有经济效益之美。统一强度理论的美还表现在它可以推广应用到许多其他领域[65]。图17.12和17.13为统一强度理论与已有的一些准则的关系。图17.13中三个极限曲线为统一强度理论产生的新的准则。

(www.xing528.com)

图17.12　统一强度理论与已有的一些准则的关系

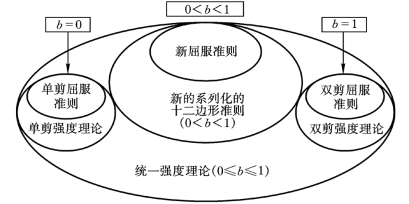
图17.13　统一强度理论包含的各种准则

由于双剪统一强度理论的这些特点，一些土力学著名专家已将它写入有关的土力学著作，并作了积极的评价[43，45-60]。例如，陈正汉教授将它作为岩土力学公理化理论成功的一个例子；郑颖人院士将广义双剪强度理论作为岩土材料的基本破坏准则之一；沈珠江院士将它作为排比法的一个例子，他在文献[60]中指出：“这一方法是把迄今为止的本领域内所有前人研究成果排列对比，找出规律性。著名的例子是元素周期表的发现。俞茂宏提出的双剪强度理论也是运用这一方法。”沈珠江于2004年在《力学进展》发表了对Unified Strength Theory and Its Applications一书的评介，评介指出，“材料力学领域内为数不多的由中国学者原创的理论得到了国际同行的承认”“俞教授的成就表明，中国学者在材料强度理论研究方面已占了一席之地，在熟知的Tresca、Mises、Mohr、Coulomb等外国人名之后多了一个中国人名”“充分显示了这一理论的实用价值和强大功能”。统一强度理论在土力学问题的应用，已经得出了很多新的结果[65-200]。