Yoshimine教授的土力学新论：方法

Yoshimine根据2006年Kiyoo Mogi对Dunham白云岩和Inada花岗岩的真三轴试验数据（图16.1）进行了计算机拟合分析。

库仑准则：

式中，β为摩擦力，C为黏聚力，τ和σ的值取决于材料本身。

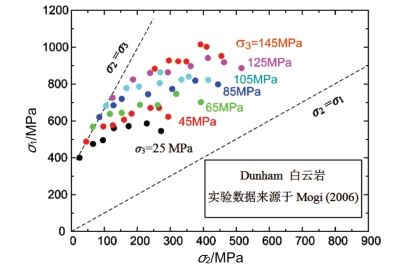
图16.1　Dunham白云岩的强度（Kiyoo Mogi 2006）

由俞茂宏教授提出的双剪模型（统一强度理论）：

其中：

图16.2为b=0时Yoshimine根据以上实验数据拟合得出的Dunham白云岩的σ13随着τ13的变化曲线。其中材料参数β=0.597，C=79.7 MPa，相关的线性拟合因素r2=0.953。

图16.2　Dunham白云岩的σ13随着τ13的变化曲线（b=0）

Dunham白云岩的统一强度理论参数b随着相关因素的变化曲线如图16.3所示，其中r2max为0.979。通过拟合，最终得出参数b的最佳值为0.4798。

图16.3　Dunham白云岩的参数b随着相关因素r2的变化曲线

不同情况下Dunham白云岩σtwin随着τtwin的变化曲线如图16.4所示，其中材料参数的拟合最佳值为：β=0.485，C=145.4 MPa，b=0.4798。

图16.4　Dunham白云岩的σtwin随τtwin的变化曲线

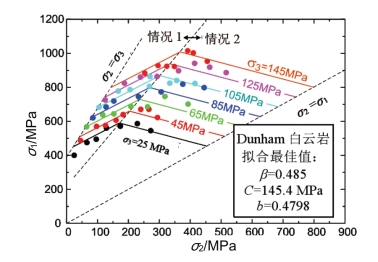
根据以上得出的材料参数，应用统一强度理论拟合不同情况下Dunham白云岩强度的结果如图16.5所示。

由材料参数拟合最佳值即可画出Dunham白云岩的屈服极限面，如图16.6所示，其中β=0.485，C=145.4 MPa，b=0.4798。

(www.xing528.com)

图16.5　Dunham白云岩的σ2随σ1的变化曲线

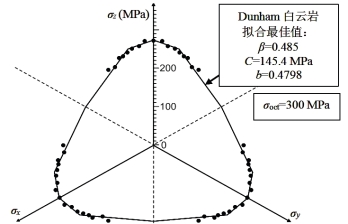
图16.6　Dunham白云岩强度的屈服极限面

2006年，Kiyoo Mogi对Inada花岗岩进行真三轴实验得出的强度结果如图16.7所示。

图16.7　Inada花岗岩的强度（Kiyoo Mogi 2006）

Yoshimine根据以上实验数据，得到Inada花岗岩的统一强度理论参数b随着相关因素的变化曲线如图16.8所示，其中r2max为0.996，得出参数b的最佳值为0.2384。

由此可得不同情况下，Inada花岗岩的σtwin随着τtwin的变化曲线如图16.9所示，其中材料参数的拟合最佳值分别为：β=0.642，C=110.7 MPa，b=0.2348。

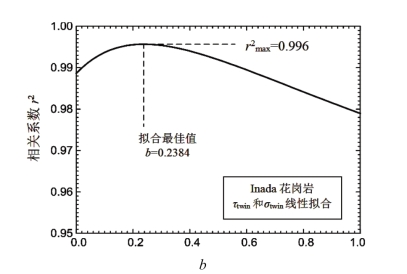
图16.8　Inada花岗岩的参数b随着相关因素r2的变化曲线

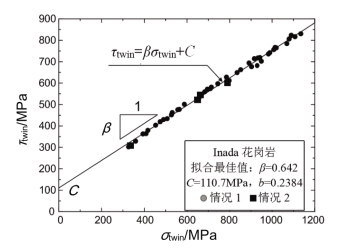
图16.9　Inada花岗岩的σtwin随τtwin的变化曲线

根据以上得出的材料参数，应用统一强度理论拟合不同情况下Inada花岗岩强度的结果如图16.10所示。

根据材料参数拟合最佳值即可得出Inada花岗岩的屈服极限面，如图16.11所示，其中材料的几个参数分别为：摩擦力β=0.642，黏聚力C=110.7 MPa，统一强度理论参数b=0.2384。为了便于对比，将Dunham白云岩和Inada花岗岩的屈服极限面绘制在同一个坐标下，结果如图16.12所示。

图16.10　Inada花岗岩的σ2随着σ1的变化曲线

图16.11　Inada花岗岩的屈服极限面

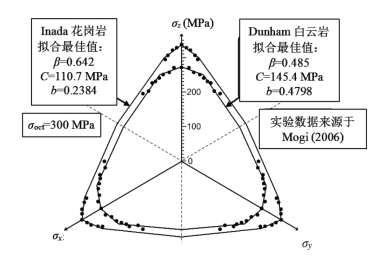
图16.12　Dunham白云岩和Inada花岗岩的屈服极限面

由此可见，对于Dunham白云岩，统一强度理论参数b的值为0.4798，而对于Inada花岗岩，统一强度理论参数b的值为0.2384。