竖井是矿山建设中的咽喉工程。竖井开挖后，井筒周围的岩体将会产生较大的附加应力。在附加应力作用下，竖井将可能因井壁发生塑性流动而破坏。因此，研究竖井的稳定性具有重要的现实意义。工程中，人们常常利用Tresca或莫尔-库仑强度准则研究竖井的稳定性。近年，宋建波等[22]采用Hoek-Brown准则研究了竖井的稳定性。这些分析没有考虑中间主应力，但实验表明，中间主应力对岩体的强度具有明显的影响[23]。
徐栓强等和侯卫[24]以统一强度理论作为岩体的破坏准则，分析了岩体中圆形竖井的稳定性，导出了竖井稳定性的判据和极限深度的方程式，并利用所得的极限深度方程式探讨了岩体拉压强度效应和中间主应力效应对竖井极限深度的影响。他们假设岩体中有一个半径为a的圆形竖井（图15.18（a）），井筒可看作是半无限体中的垂直圆孔。沿距地表Z处取厚度为dZ的薄层，该处由自重引起的垂直应力pv=−γz，水平应力ph=−λγz，其中γ为岩体容重，λ为岩体的侧压比。该薄层可看作含圆孔的大薄板，如图15.18（b）所示。
图15.18 竖井及其计算简图
离井筒中心r处的围岩应力为：
将关系式r=a代入上式，得出井壁处的应力为：σr=0，σθ=−2λγz，σz=−γz。用
分别表示竖井井壁处单元体的最大、中间以及最小有效主应力，则有：
当λ≤0.5时：
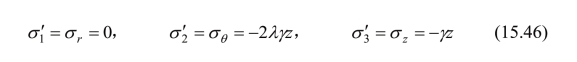
当λ＞0.5时：
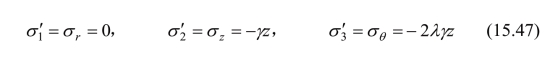
对于λ≤0.5的情况，根据统一强度理论公式（15.28）可知，当井壁处于稳定的极限状态时，应力分量应满足下列条件：
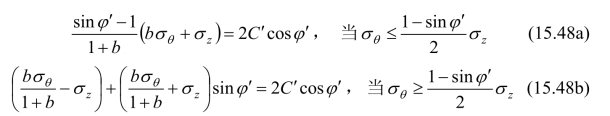
对于λ＞0.5的情况，处于稳定的极限状态的竖井，其井壁的应力分量应满足：
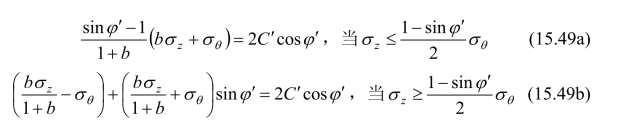
以上利用有效应力统一强度理论，导出了竖井井壁处于稳定极限状态时，竖井井壁处的应力应满足的条件。根据这些条件，可解得竖井保持稳定状态时竖井的最大深度。
作为例子，下面计算位于原岩初始应力为静水压力岩体中的圆型竖井的极限深度，并且讨论岩体的内摩擦角φ′和中间主应力效应对竖井的极限深度的影响。对于这种情况，λ=1>0.5，由式（15.47）可得竖井井壁处的应力为：
(www.xing528.com)
显然，上面的应力满足σz≤（1−sinφ′）σθ/2。
根据式（15.49a），可解得竖井保持稳定的最大深度Zmax为：
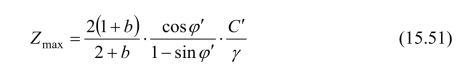
竖井保持稳定的最大深度Zmax，又称为竖井稳定的极限深度。如果竖井深度小于上面所得极限深度Zmax，则竖井不会因井壁发生塑性流动而破坏；相反，若竖井深度大于Zmax，竖井将因井壁发生塑性流动而破坏。根据极限深度Zmax，我们可判断实际竖井的稳定性，进而采取合理的支护措施以保证竖井的稳定。
可以看出，上面所得的竖井极限深度Zmax的方程式（15.51），考虑了岩体强度内摩擦效应及中间主应力效应等。当给定材料参数φ′以及b的值时，可得相应竖井的极限深度。若取b=0，由式（15.51）得到基于莫尔-库仑强度准则的结果：
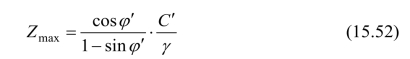
它忽略了岩体的中间主应力效应。若材料参数φ′=0，则得出基于统一屈服准则的结果为：
它忽略了岩体的内摩擦效应。若同时取材料参数φ′=0，b=0，则可得：
这是基于Tresca准则的结果，它忽略了岩体的中间主应力效应以及内摩擦效应。因此，莫尔-库仑强度准则和Tresca准则的结果均是本书结果的特例。
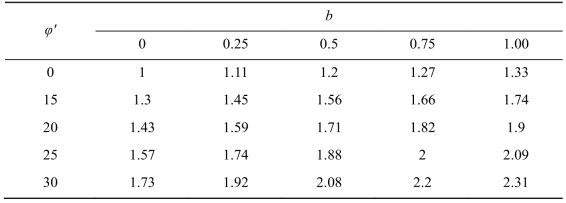
表15.3给出了内摩擦角φ′分别等于0°、15°、20°、25°和30°，统一强度理论参数b分别等于0、0.25、0.5、0.75和1.00时，竖井极限深度Zmax/（C′/γ）的值。可以看出，竖井极限深度Zmax随着中间主应力系数b的增大而增大，莫尔-库仑强度准则给出最小的极限深度，广义双剪准则给出最大的极限深度。另外，岩体的内摩擦角φ′越大，求得的Zmax也越大。因此，分析竖井稳定性时，忽略岩体的拉压强度差效应和中间主应力效应将会低估岩体的承载能力。
上面针对原岩初始应力为静水压力的情况讨论了竖井的极限深度，当原岩初始应力不是静水压力时，也可进行类似的讨论。
表15.3 统一强度理论下竖井的极限深度Zmax（Zmax=C′/γ）
以上是徐栓强和侯卫[24]采用统一强度理论对圆形竖井稳定性的分析结果。他们导出了圆形竖井稳定的判据和极限深度的算式，能够定量地考虑岩体的拉压强度差效应、中间主应力效应等，因而能适用于多种岩体。研究表明，竖井的极限深度随中间主应力系数b和岩体的内摩擦角φ′的增大而增大，因此，考虑材料的拉压强度差效应和中间主应力效应有助于发挥其强度潜能。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
