自然状态下的黄土往往可以保持几乎垂直的切割面。图14.18是西安青龙寺附近的人工垂直切割的黄土边坡(吉嶺充俊2004)。曾经很多人对直立边坡问题进行过研究,例如Chen和Mizuno(1990),Pastor、Thai和Francescato(2000),Zimmermann和Commend(2001)等。Tresca准则、Mises准则、莫尔-库仑准则、Drucker-Prager准则等作为破坏准则被用于直立边坡的分析,但是Postor等指出,直立边坡的精确解仍然是未知的。

图14.18 西安青龙寺附近的人工垂直切割的黄土边坡(吉嶺充俊 2004)
2004年,吉嶺充俊教授对图14.18中人工垂直切割的黄土边坡的原始黄土力学特性进行了研究。他们采集原始黄土(图14.19)进行空心圆柱试件复合应力实验,所用仪器为东京大学型中空试件压缩扭转复合应力试验机(图14.20)。青龙寺黄土的空心圆柱复合应力实验结果如图14.21所示[20]。

图14.19 西安青龙寺原始黄土试样的采集

图14.20 东京大学型中空试件压缩扭转复合应力试验机
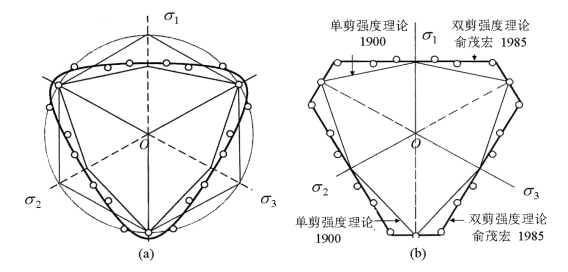
图14.21 青龙寺黄土的空心圆柱复合应力实验结果。(a)Yoshimine准则的对比;(b)统一强度理论的对比
图14.21给出了青龙寺黄土复合应力实验与Yoshimine准则和统一强度理论的对比结果。可以看到,Yoshimine准则和统一强度理论两种极限线都可以与实验结果匹配。
为了便于各种准则的比较,采用统一强度理论的三个典型准则,即b=0、b=1/2和b=1计算了西安青龙寺附近的黄土垂直边坡的临界直立高度。黄土垂直边坡的材料参数为:γ=1.6×104 N/m3,C=18 kPa,φ=30°。垂直边坡的应力场如图14.22所示。
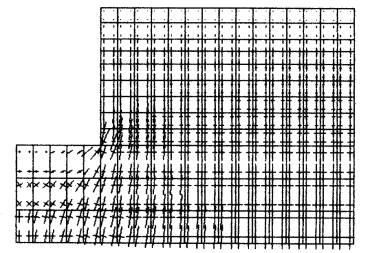
图14.22 垂直边坡的应力场
使用统一强度理论的三个典型准则计算黄土直立边坡的临界直立高度,结果分别为:
(1)统一强度理论b=0(单剪强度理论),Hp=6.4 m;(https://www.xing528.com)
(2)统一强度理论b=0.5(新准则),Hp=7.9 m;
(3)统一强度理论b=1(双剪强度理论),Hp=9.2 m。
计算的临界高度的分析结果如图14.23所示,其中统一强度理论b=1的结果最接近图14.18所示的青龙寺实际黄土边坡。
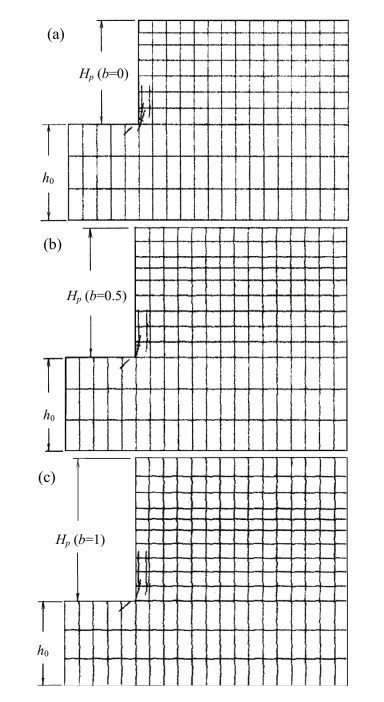
图14.23 黄土直立边坡的临界高度。(a)b=0,Hp=6.4 m;(b)b=1/2,Hp=7.9 m;(c)b=1,Hp=9.2 m
直立边坡也可采用强度折减法进行分析。马宗源和廖红建[21]采用统一强度理论对直立边坡的安全系数进行了研究。图14.24(a)为直立边坡的模型示意图。按20×20网格密度采用相关联流动法则进行计算,计算参数取值:弹性模量E=100.0 MPa,泊松比v=0.3,重度γ=20.0 kN/m3,黏聚力C=30.0 kPa,内摩擦角φ=30°。
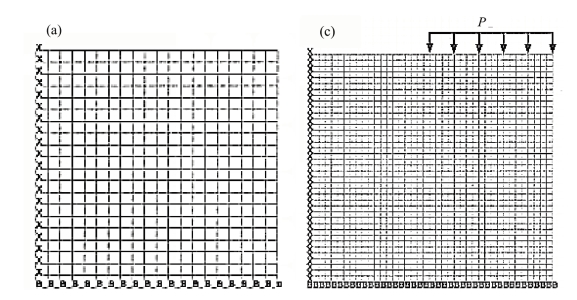
图14.24 直立边坡的模型及网格划分
图14.25为边坡位移矢量图。可以看出,在重力作用下,直立边坡滑动面随边坡土体中间主应力效应的增大而逐渐深入坡体,即滑动的坡体有所增加。从图中还可以看出,参数b越大,土体到极限状态时的范围越大,也就是有更多的土体发挥其强度潜力。
从图14.25三种结果的对比还可以看到,采用参数b=0的准则计算的极限载荷最小,相应的塑性区面积也最小;采用参数b=1的准则计算的极限载荷最大,相应的塑性区面积也最大。这表明土体结构有更多部位的材料参与到极限状态,并发挥出自己的强度潜力,从而使结构整体的极限载荷得到提高。
马宗源也对直立边坡坡顶受均布荷载时影响边坡破坏模式的因素进行了分析。他建立的直立边坡模型如图14.24(b)所示,采用竖向位移荷载模拟刚性粗糙基础压力,通过荷载位移曲线确定边坡的极限荷载。图14.26为采用不同强度准则及流动法则计算出的直立边坡荷载位移曲线,可以看出不同准则计算结果差异较大,反映了中间主应力效应对边坡坡顶极限承载力存在较大影响。
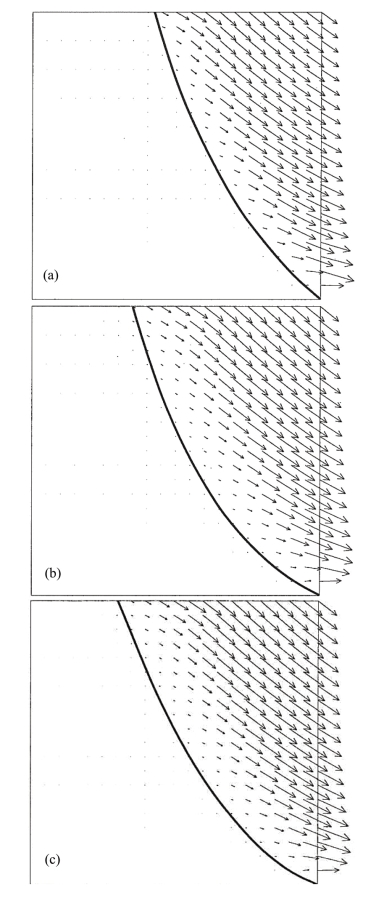
图14.25 边坡位移矢量图。(a)b=0,安全系数=1.09;(b)b=0.5,安全系数=1.32;(c)b=1,安全系数=1.48

图14.26 直立边坡在不同强度准则下的荷载和位移关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




