边坡滑移线场解的统一统计-土力学新论

在工程实践中，采用莫尔-库仑强度理论进行极限分析时，因该理论没有考虑中间主应力的影响，其结果对某些材料有所偏差。它只适用于剪切强度极限τ0与拉伸强度极限σt和压缩强度极限σc的关系为τ0=σtσc/（σt+σc）的材料。双剪强度理论则只适用于τ0=2σtσc/（σt+2σc）的材料。采用统一强度理论和统一滑移线场理论对边坡的极限荷载进行分析，可以求得结构的统一解。

已知边坡处于平面应变状态，其中坡角∠BAE=γ>π/2，材料拉压强度比α=σt/σc，AB面作用着均匀垂直荷载p，如图14.16所示。试求作用于AB面的极限荷载pu。对于平面应变塑性情况，可采用滑移线法对楔体作塑性极限分析。边坡滑移线场如图14.16所示。

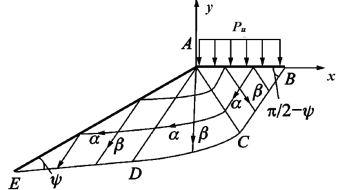
图14.16　边坡滑移线场

根据平面应变统一滑移线理论和图14.16的滑移线场，可以求得作用于AB面的极限荷载的统一解pUST为：

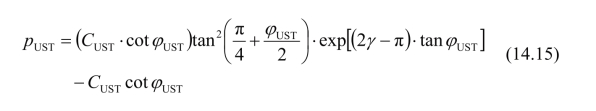
参数φUST和CUST反映了统一强度理论中间应力系数b的效应。因此，正是在引进了参数φUST和CUST来代替φ0和C0后，中间主应力效应才得以反映在式（14.15）表示的边坡极限荷载pUST中。材料两类参数可以相互换算，即α=（1−sinφ）/（1+sinφ），σt=2Ccosφ/（1+sinφ）。

如果材料的内摩擦角φ0=0，则统一强度理论的材料参数简化为φUST=0，CUST=2C0（b+1）/（b+2）。

计算实例：(www.xing528.com)

如果边坡的坡顶角γ=0.8π时，取材料的拉压强度比为三种比值α=σt/σc=0.3，α=0.5，α=0.8。边坡极限承载力pUST与b的关系曲线如图14.17所示。

当b=0时，φUST=φ0，CUST=C0，此时统一解将退化为典型的莫尔-库仑解，即：

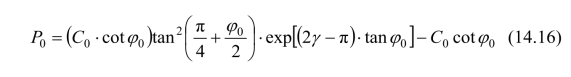
当b=0，α=1时，即可得出经典塑性理论中服从Tresca屈服准则材料的楔体的极限荷载：

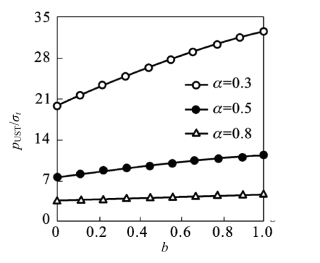
图14.17　边坡极限荷载pUST与统一强度理论参数b的关系曲线

世界各国学者对边坡稳定性问题进行了大量研究，取得了丰富的研究成果。各种理论、方法精彩纷呈。由以上分析可知，边坡稳定性分析的统一解不是一个解，而是一系列的结果，这种系列化的结果可以更好地适合于不同的材料和结构。统一解可以为工程应用提供更多的比较、资料、参考和合理选用，目前已经有一些不同的研究结果。