土力学新论：梯形结构统一滑移线解

讨论边坡的稳定性，一般按平面应变问题考虑。平面应变的统一强度理论如式（14.1）和（14.2）所示。梯形结构如图14.12，坡顶角为2ξ，顶部有均布荷载，且2ξ分别等于120°、80°和60°时，结构的极限承载力q可以由俞茂宏于1997年提出的平面应变统一滑移线场理论计算得出[21]。

图14.11　有渗流时计算图示

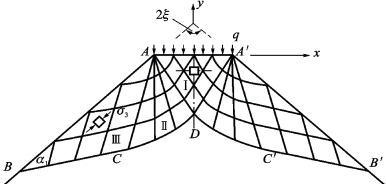
图14.12　梯形结构的滑移线场

图14.12所示的路堤结构的极限承载力q的统一解，如式（14.12）和图14.13所示[21]。图14.14表示了角2µ（即滑移角）随参数b的变化而变化的关系曲线。

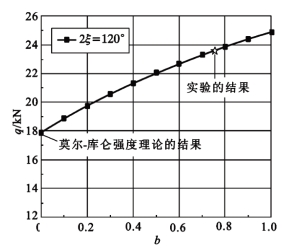
图14.13　极限荷载统一解的系列结果(www.xing528.com)

图14.14　不同参数b值时的滑移角

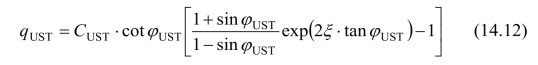
有意义的是，式（14.12）在形式上与传统的土力学中的结果相同，但是公式中的材料参数（黏聚力参数C0和摩擦角φ0）变化为统一强度理论的新的统一参数CUST和摩擦角φUST[25]。

由此可以给出一系列新结果。图14.13为应用统一强度理论和统一滑移线场理论分析一个梯形结构得出的一系列结果。传统解（b=0）是其中的一个特例。图中同时给出一个坡顶角2ξ=120°的梯形结构模型的实验比较，实验结果在横坐标b=0.75处，而传统的莫尔-库仑强度理论得到的结果在横坐标b=0处。可以看到，统一强度理论的结果不仅为不同的材料和结构提供了更多的资料、参考和选择，并且可以更好地符合实验的结果（b=0.75）。其与莫尔-库仑强度理论（b=0）相比，提高结构的承载能力31%，可以取得显著的经济效益。

当坡顶角2ξ=180°时，路堤结构即为条形基础的受力状态，式（14.12）简化为条形地基的极限承载力的统一公式：