圆形基础地基承载力极限

以上为拉压强度相同材料（φ0=0，即σt=σc）的轴对称统一特征线理论的分析。同理，对于拉压强度不同材料（φ0≠0，即σt≠σc），也可以求得空间轴对称结构极限承载力的统一解。图13.11为一圆形地基，地基材料为各向同性土体，材料参数如下：C0=0.03 MPa·s，φ0=15°。结构为在表面受压的半无限体，受压面光滑且半径为2 m，分析其极限荷载。

图13.11　受均匀压力作用的土体及其空间轴对称特征线场

(www.xing528.com)

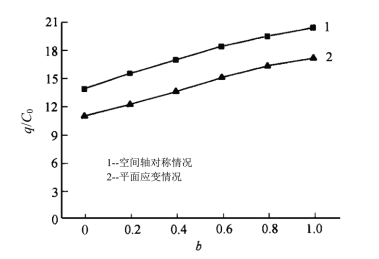
图13.12　圆形地基极限荷载q和参数b的关系曲线

对于半无限空间的轴对称特征线问题，采用统一轴对称特征线场理论计算参数b=1时的空间轴对称特征线场（右半部分），如图13.11所示。对于半无限空间的轴对称特征线问题，计算得到极限荷载q/C0和参数b的关系曲线，如图13.12曲线1所示（计算过程略）。所得的荷载在b=0时与文献[18]中基于Haar-von Karman假设和莫尔-库仑强度理论的Cox（1961）完全解（q/C0=13.9）是一致的，Cox解为b=0的一个特例。作为对比，图中同时给出半无限空间的平面应变滑移线的结果，计算得到极限荷载q/C0和参数b的关系曲线如图13.12的曲线2所示[11]。

空间轴对称统一特征线理论可以得出一系列拉压强度不同（φ0≠0）以及拉压强度相同（φ0=0）的材料采用不同的强度理论的结果。文献中采用Tresca屈服准则对于拉压强度相同（φ0=0）的材料的解[18]和采用莫尔-库仑强度理论对于拉压强度不相同（φ0≠0）的材料的解[17]，分别为统一特征线场理论b=0时φ0=0和φ0≠0的特例。