圆锥台顶面均匀受压时特征线场及极限荷载-《土力学新论》

以下应用俞茂宏、李建春等2001年提出的轴对称统一特征线场理论，分析一个圆锥台在顶面均匀受压时的特征线场及极限荷载。此圆锥台顶面光滑，半径20 mm，侧面自由边倾斜角为45°。材料参数：E=2.1×105 MPa，C0=12 MPa•S，φ0=0。因为轴对称，可以只考虑圆锥台的一半（图13.8）。

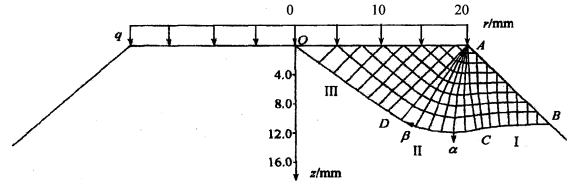
图13.8　圆锥台在顶面均匀受压时的特征线场

采用统一轴对称特征线场理论计算。由于φ0=0，所以φUST=0，可得µ=π/4，即该材料的特征线相互正交。符合这种情况的特征线方程为：

应力控制微分方程为：

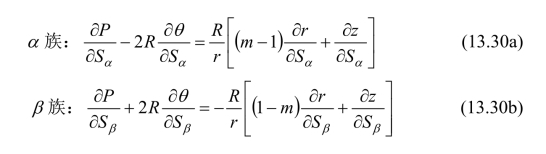
取参数m=0.5，式（13.30）中用差分代替微分，并进行数值积分。应力场分为3个区域I、Ⅱ、Ⅲ，边界分别为边AB和AC、AC和AD、AD和AO。首先由无应力边AB开始计算并构造区域I的特征线场，定出这里的P和θ。由于材料均匀且各向同性，在AB边上有P=−R，σ1=σ2=0，σ3=2R，θ=3π/4；在区域Ⅱ中，由于点A为奇异点，所以通过A点的α族和与其垂直的β族特征线所形成的中心扇形构成该区域的特征线场；区域Ⅲ的特征线场由AO边和AD边决定，在边界AO上有θ=0。通过差分计算可得出一系列不同倾斜角、C值、φ值和b值的特征线场。根据区域Ⅲ中的特征线场、AO边的边界条件和平衡条件可以求得顶面上的极限均布压荷载q，如图13.9所示。作为对比，图中同时给出了按统一平面应变滑移线场理论的计算结果。可以看出，两者随不同屈服准则而变化的规律是一样的。图13.8表示顶角为45°的锥体及其特征线场（当参数b=1，即为双剪屈服准则解）。(www.xing528.com)

为了验证，用基于统一强度理论的统一弹塑性有限元程序UEPP中的统一强度理论材料模型对该圆锥台进行计算，求得顶面上极限荷载q，并和用统一特征线场理论求得的顶面上极限荷载q进行比较。图13.9为圆锥台极限荷载q随强度理论参数b的变化曲线。从图中可以看出，用统一特征线方法计算的结果和用有限元计算的结果相当接近。用统一特征线场方法计算得到的统一解为一系列结果。当参数b=0时，即为采用单剪屈服准则（Trsca屈服准则，1864年）的解；当参数b=1时，即为采用双剪屈服准则（俞茂宏，1961）的解。用统一特征线场方法计算得出：当b=0.8时的极限荷载系数为q/2C0=1.968，与文献[30]的实验结果（q/2C0=1.96）相符。

对于图13.8所示梯形横截面的平面应变和空间轴对称情况，用有限元程序UEPP中的统一强度理论材料模型，求得当参数b=1时顶面中点O处荷载q0与位移δ的关系，其结果如图13.10所示。可以看出，轴对称状态下锥体承受极限荷载略大于平面应变状态的解，符合图13.9所示的特征线结果。对于图13.10中的空间轴对称状态，O点的极限荷载接近于图13.9中特征线法在参数b=1的值。由此可见，用统一特征线方法计算空间轴对称问题在理论上是可靠的，在应用中是可行的。

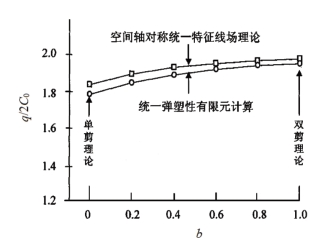
图13.9　圆锥台极限荷载与参数b的关系曲线

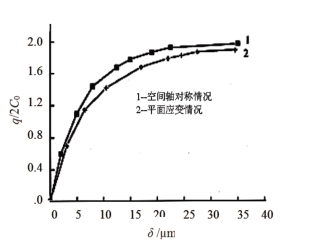
图13.10　O点位移和荷载的关系曲线