统一轴对称特征线场理论–资料来自《土力学新论》

对于一般的轴对称问题，存在应力分量σt、σθ、σz和τrz，其余应力分量为零，即τθr=τθz=0，所以σθ一定为主应力。根据空间轴对称应力状态的特点，我们引入：

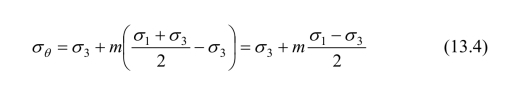
式中，m为引入的参数，0≤m≤2。当m=0或m=2时，为Haar-von Karman完全塑性条件，即Haar-von Karman完全塑性条件为式（13.4）的一个特例。

在轴对称问题中，令：

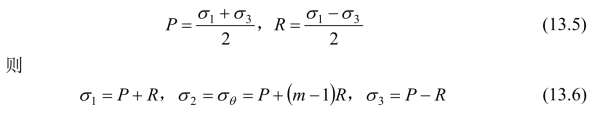
所以空间轴对称问题中的应力分量为：

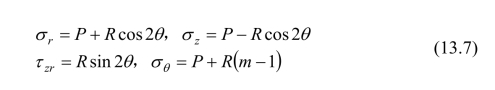
式中，θ为最大主应力和r轴的夹角。由于m−1≤sinφ0，即σ2≤P+Rsinφ0，符合统一强度理论公式第一式的条件，将式（13.6）代入统一强度理论方程式（13.2a）中，得：

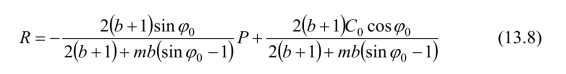
式（13.8）可简写为：

式中，φUST和CUST分别为采用统一强度理论得出的统一摩擦角和统一黏聚力，它们可以表述为统一强度理论参数b的函数。

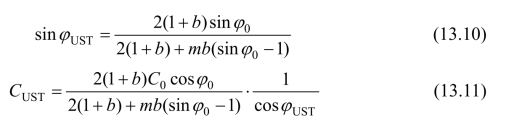
当m=0.5时，sinφUST和CUST可表示为：

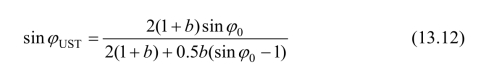
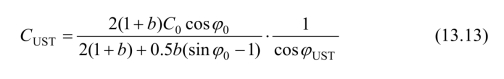
式（13.13）中的统一特征线场参数φUST和CUST与常用的材料参数φ0和C0之间的关系如图13.6和13.7所示，图中曲线分别表示φ0=5°、φ0=10°、φ0=15°、φ0=20°、φ0=25°的变化规律。

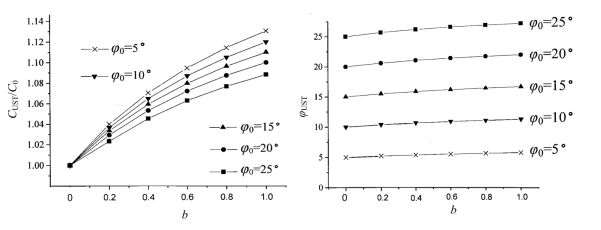
图13.6　统一凝聚力CUST随b的变化曲线 图13.7 统一摩擦角φUST随b的变化曲线(www.xing528.com)

当P取压应力时，式（13.9）可转化为：

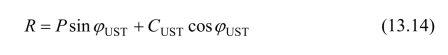
轴对称问题的平衡微分方程为：

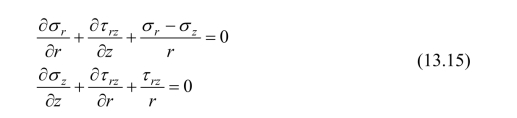
将式（13.7）和（13.14）代入上式，得出应力控制微分方程为：

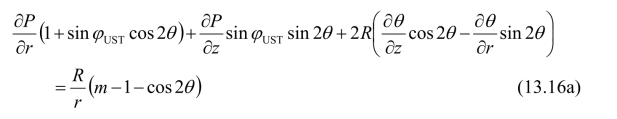
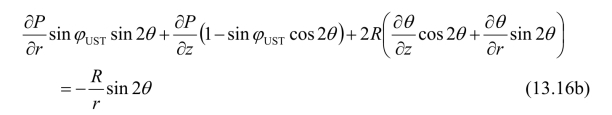
假定在平面rOz上，沿某一曲线z=z（r）给定了函数P和θ，则：

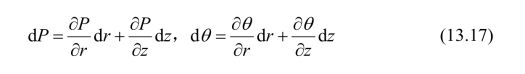
联立式（13.16）和（13.17）得出的特征线方程为：

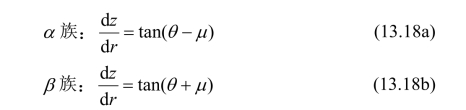
式中，2µ为α和β线之间的夹角，它们之间的关系为µ=π/4−φUST/2。

根据方向导数公式，得柱坐标与随体坐标的关系为：

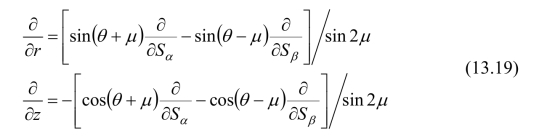
将式（13.16）化为曲线关于随体坐标Sα和Sβ的形式，得：

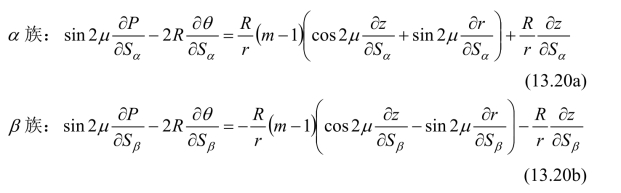
上式即为轴对称特征线理论的应力场关系式。