地基极限承载力公式推导-《土力学新论》研究成果

1.基本假设

如图11.43所示，当地基发生整体剪切破坏时，其滑动面一直延伸至地面并交于E点，而滑动面则由直线AC、对数螺旋曲线CH和直线HE三部分组成，其中AC与水平面成45°+φUST/2。基础侧面BF与土体之间的相互作用以及基础两侧BEF土体重量的影响，可由BE平面上的等代应力σ0和τ0来代替。因此，在考虑土体的平衡时可以将BEF的土体移去，并用“等代自由面”BE来代替，假定BE面与水平面的夹角为β，它随基础的埋深而增加。

图11.43　地基极限承载力模型

基础侧面上的法向应力σα按静止压力分布，若基础侧面与土之间的摩擦角为δ，则作用于基础侧面上的平均法向应力σα和切向应力τα为：

式中，k0为土的静止侧压力系数；γ为基础底面以上土的容重；D为基础的埋置深度。

2.黏聚力和基础两侧土的超载引起的承载力

（1）等代自由面BE上法向应力σ0和切向应力τ0的计算

由BE面法线方向所有力的平衡条件可得BE面上的法向应力为：

同理，BE面切向应力为：

由对数螺旋曲线性质及图11.43中的BHE的几何关系得：

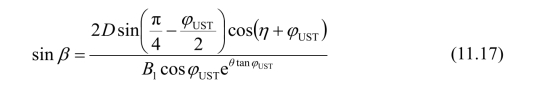
式中，θ为对数螺旋曲线的中心角（θ=135°+β−η−φUST/2）。

从式（11.15）和（11.16）可知，BE面上的法向应力σ0和切向应力τ0是β的函数，因此在求解时要进行试算，即先假定β值，由式（11.15）和（11.16）算出σ0、τ0，再通过图11.44上的极限应力图求解β值，最后再由式（11.17）反算β，直至假定值与反算值两者相符。

（2）H面的法向应力σb和切向应力τb的计算

由图11.44可知：

由几何关系可得：

由于BH面处于极限平衡状态，故切向应力τb和σb的关系为：

图11.44　莫尔圆

将式（11.20）代入式（11.19）可得：

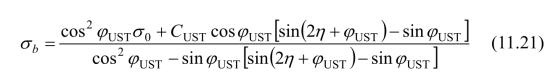(www.xing528.com)

（3）BC面上的法向应力σc和切向应力τc计算

如图11.45所示，BCH面上所有各力对B点的力矩之和为零，可得BC面上的法向应力为：

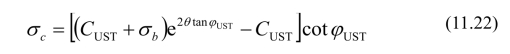
由于BC面处于极限状态，该面的切向应力与法向应力的关系为：

如图11.46所示，将三角楔体ABC作为考察对象，列出竖向力的平衡方程为：

图11.45　BCH面上所受的力

图11.46　力学模型

将式（11.21）−（11.23）代入式（11.24）可得极限承载力为：

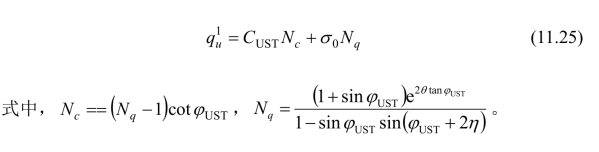
3.由土重引起的极限承载力

此时假定土的凝聚力和基础两侧超载等于零，即C0=0，σ0=τ0=0，对数螺旋曲线中心移到O点并需通过试算确定。现以图11.43左侧中的ACHG为研究对象，通过O点合力矩等于零，可求得AC面上的被动土压力为：

式中，p为AC面上的被动土压力；W为土体自重；p1为GH面上的被动土压力。

如图11.47所示，由ABC上的作用力在竖直方向的平衡条件，可得到由土重产生的承载力为：

式中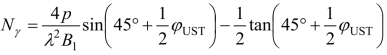，，γ为基底以下地基土的容重；B1为基底宽度；Nγ为承载力系数。

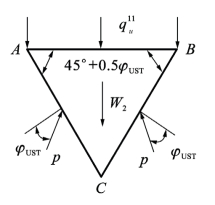
图11.47　力学模型

最后将式（11.25）和（11.27）叠加，即得条形基础在中心荷载作用下均质地基的极限承载力：

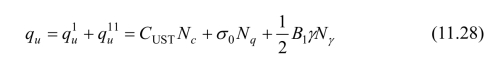
式（11.28）的系数Nc、Nq、Nγ均与φ0、β、η有关，而η受到“等代自由面”上抗剪强度动用系数的控制。从图11.46中的几何关系得η和n的关系为：

式中，n为抗剪强度动用系数。