统一强度理论可表示为：
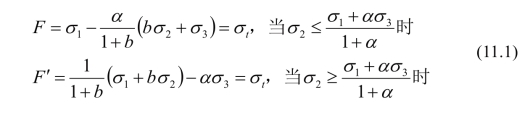
式中，α=σt/σc为材料的拉压比，b为统一强度理论中的反映中间主剪应力及相应面上的正应力对材料破坏影响程度的参数。σt为岩土体的抗拉强度，σc为岩土体的抗压强度。σt、σc、b和α都由实验确定。
1.基本假设
（1）基础底面粗糙。当地基发生整体剪切破坏并形成延伸至基底平面高程处的连续滑动面时，基底以下有一部分土体将随基础一起移动而始终处于弹性状态，该部分土体为弹性楔体。弹性楔体的边界ab为滑动边界的一部分，并假设与水平面的夹角为ψ，如图11.3所示。
除弹性楔体外，在滑动区域范围内的所有土体均处于塑性状态，滑动区由径向剪切区Ⅱ和朗肯被动区Ш组成。径向剪切区的边界bc由对数螺旋曲线表示：
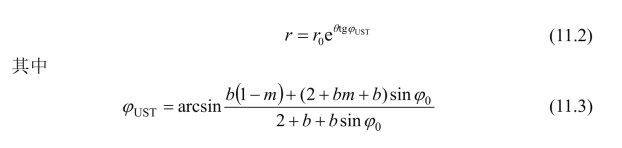
式中，m=2σ2/（σ1+σ3），φ0为岩土体材料的内摩擦角，r0为起始矢径，θ为任一矢径与起始矢径r0的夹角。朗肯被动区Ш的边界cd为直线与水平面成角45°+φUST/2，如图11.4所示。
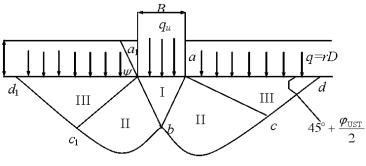
图11.3 粗糙基底图
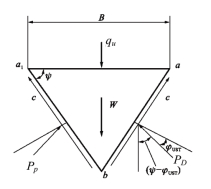
图11.4 弹性楔体力学模型
（2）不考虑基地以上基础两侧土体的抗剪强度的影响，而用相应的均布荷载q=rD表示。
2.地基极限承载力的确定
根据上述基本假定，由图11.4中的弹性楔体aba1的平衡条件可得整体剪切破坏时的极限荷载：
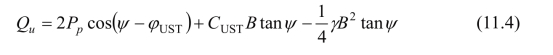
其中
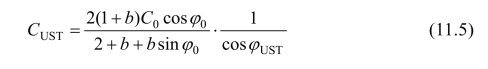(www.xing528.com)
式中，C0为岩土体材料的黏聚力，B为基础宽度，γ为地基土的容重，Pp为作用于弹性楔体边界面ab上的被动土压力的合力，即：
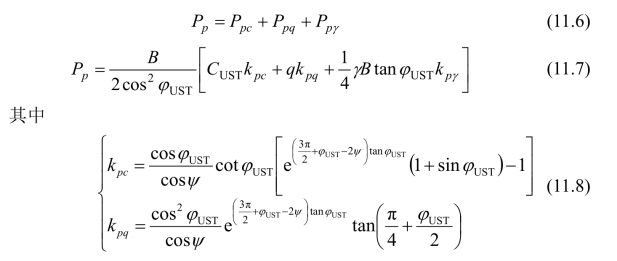
式中，kpγ为γ项的被动动土压力系数，须通过试算确定。
将式（11.6）和式（11.7）代入式（11.4）可得：
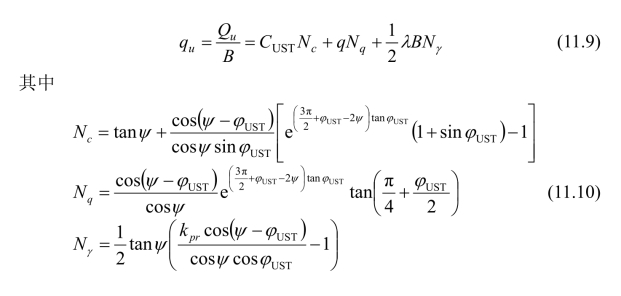
式（11.9）是在基底粗糙的条件下得到的，其中弹性楔体边界ab与水平面的夹角ψ为未定值。为此本节作如下假定：
（1）假定基础完全粗糙（图11.5）。此时可假定弹性楔体边界ab与水平面的夹角为ψ=φUST，则式（11.10）可以写成如下形式：
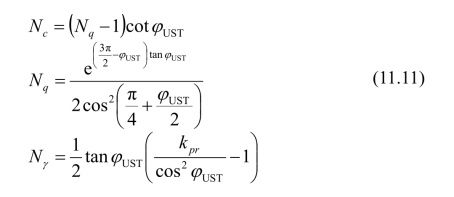
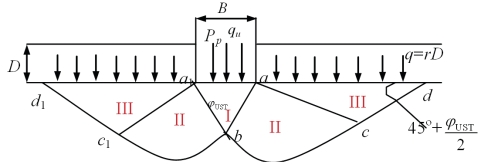
图11.5 完全粗糙基底
从上式知承载力系数均与内摩擦角有关，被动土压力系数kpγ须试算确定。为了便于计算，结合太沙基经验公式，有：
（2）假定基底完全光滑（图11.6）。此时弹性楔体成为朗肯主动区，并且整个滑动区域已演变为与普朗特尔完全相同。朗肯主动区的边界与水平面的夹角为ψ：
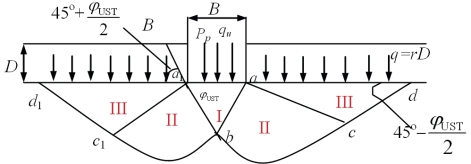
图11.6 完全光滑基底
将式（11.12）代入式（11.9），则可求出基础完全光滑的承载力系数Nc、Nq和Nr。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
