基于统一强度理论可以导出土压力理论的统一解，其计算的基本假定是[12]：
（1）墙后土体为均质各向同性的无黏性土；
（2）属平面应变问题；
（3）土体表面为一平面，与水平面成β角；
（4）主动状态：挡土墙在土压力的作用下，背离土体方向变形，从而使土体达到极限平衡状态，形成滑裂面
（图10.6）；被动状态：挡土墙在土压力的作用下，向土体方向变形，使得土体达到极限平衡状态，形成滑裂面
。
（5）在滑裂面上的力满足极限平衡关系T=NtanφUST ；在墙背上的力满足极限平衡关系T=N′tanδ。式中，φUST为土的统一内摩擦角，δ为土与墙之间的墙背摩擦角。
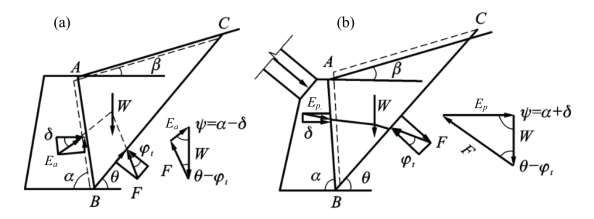
图10.6 土压力计算简图。（a）主动状态；（b）主动状态
根据滑楔的平衡关系，可以求得：
。
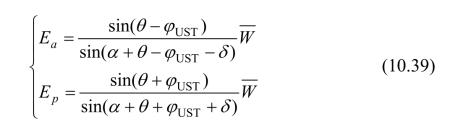
从式（10.39）可以看出，Ea和Ep都是θ的函数，其主动土压力必然产生在使Ea为最大的滑楔面上，而被动土压力必然产生在使Ep为最小的滑楔面上。因此，将Ea与Ep分别对θ求导，求出最危险的滑裂面，即可求得主动与被动土压力为：
式中，
为滑楔自重。可由式（10.39）求得：
式中，γ为土体的重度；h为挡土墙的高度；Ka和Kp分别为主动与被动土压力系数，可由下式表示：(www.xing528.com)
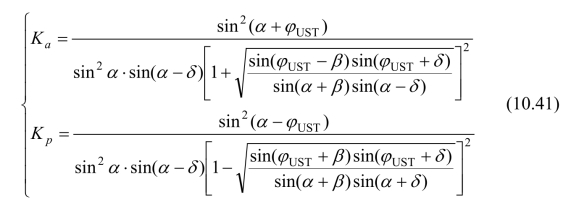
土压力的方向均与墙背法线成δ角，但与法线所成δ角的方向相反（图10.6）。当土压力作用点没有超载时，均为离墙踵高H/3处。
当墙顶的土体表面作用有分布荷载q时（图10.7），则滑楔自重部分应增加超载项，即：
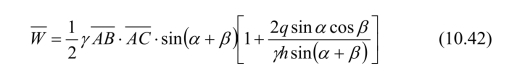
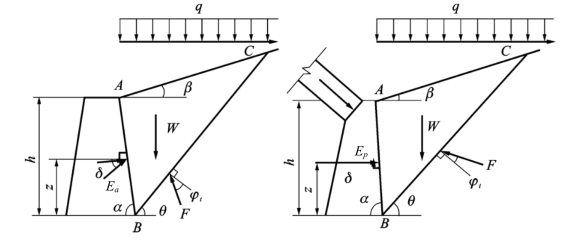
图10.7 具有地表分布荷载的情况
令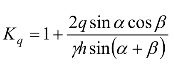
，则式（10.42）可写成：
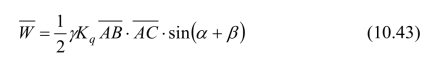
同理，可求得主动与被动土压力为：
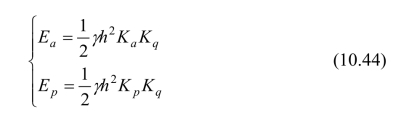
其土压力的方向仍与墙背法线成δ角。土压力的作用点位于梯形的形心，离墙踵高为：
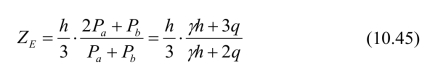
式中，Pα和Pb分别为墙顶与墙踵处的分布土压力。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
