西安古城墙东门楼基沉降研究报告

在西安东城门城楼的修复工程中，俞茂宏与西安文物局再次合作，对东城门城楼的结构力学特性和地基承载力进行了研究。参加者有王源、赵均海和杨松岩。王源和杨松岩参加了统一强度理论弹塑性有限元程序的修改、补充和调试工作。王源、俞茂宏、杨松岩和赵均海对城墙进行了动静力有限元分析。图9.25为东城门城楼台基有限元计算模型。

图9.25　西安古城墙东城门城楼台基有限元计算模型

将屋面荷载折算成作用在柱子上的集中荷载，当为三排柱时作用在每个柱子上的荷载为N=137.5 kN。所用材料的性质为明代土：E=69000 kPa，泊松比ν=0.347，C=36.3 kPa，摩擦角φ=25.65°；明代砖：E=2.23×106 kPa，泊松比ν=0.1，σ压=3225 kPa，σ拉=289 kPa。取城楼台基的典型平面，三排柱子简化为三个集中力作用在城墙上（图9.25）。城楼台基的主要材料为夯实黄土。一般采用的屈服准则如图9.26所示。其中曲线1为1900年提出的莫尔-库仑的单剪理论，它是所有屈服准则的下限；曲线2为1985年俞茂宏提出的双剪理论，它是所有屈服准则的上限；其他曲线2、3、4、5均为介于这两者之间的曲线准则。城楼台基土体的屈服准则采用俞茂宏统一强度理论中参数b=0、b=1/2和b=1的上、中、下三个准则，如图9.27所示。它们代表了所有屈服准则的上、中、下三个典型屈服准则。图9.27中左上的屈服曲线则代表了5种典型的准则。

图9.26　不同的屈服准则

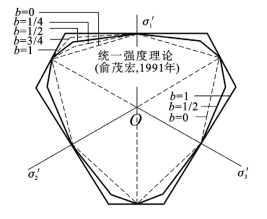
图9.27　统一强度理论的几个基本屈服准则

对东门城墙进行动静力有限元分析得出的结果如下所述。进行分析计算得出各点在至各方向的位移和荷载系数关系为f=F/N，F为分步加载的瞬时荷载，P（结构荷载）=∑N=137.5×3=412.5 kN。其中城墙顶部左边1037点的位移与荷载系数的关系如图9.28所示，城墙顶部1053点的位移与荷载系数的关系如图9.29所示。

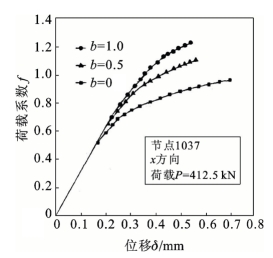
图9.28　城墙1037点的荷载位移关系

图9.29　城墙1053点的荷载位移关系

可以看出，强度理论的选择对计算结果有很大影响，统一强度理论（见第5章）为研究这种影响提供了有力的理论基础。(www.xing528.com)

图9.30给出了东门城墙在b=1时的主应力迹线图，图中表现的是主应力方向和大小的相对值。城墙顶部1061点的位移与荷载系数的关系如图9.31所示。图9.32给出了东门城墙在b=1时的变形图，该图同样反映了各个结点变形的相对大小[23-24]。

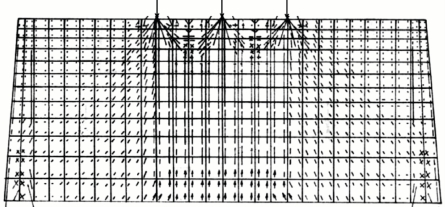
图9.30　东门城墙的主应力迹线图

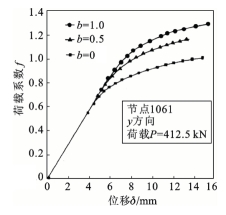
图9.31　城墙1061点的荷载位移关系

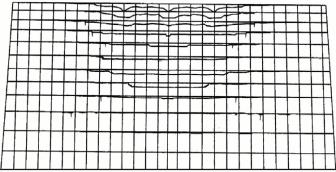
图9.32　城墙变形图

从以上分析可知：

（1）不同的屈服准则下，荷载系数不同，变形的定量描述可以从荷载-位移曲线图中得到。从图中可以反映出统一强度理论中采用不同的参数b值的影响。根据图9.31，采用不同强度理论得出的荷载系数相差很大，在三种屈服准则下的荷载系数分别为：f1=0.9（b=0）、f2=1.1（b=1/2）和f3=1.2（b=1），最大相差达33.3%。这表明考虑中间主应力效应后，将提高结构的极限荷载，这一结论与一些岩土工程的实际结果相符合。因此，合理选择统一强度理论参数b值对充分利用材料很重要。统一强度理论为这种合理选用提供了理论基础。

（2）在加载点附近的变形较大，远离加载点时的变形较小。竖向荷载作用下，竖向位移随荷载增大而增大，对水平方向的变形影响较小。

（3）荷载作用点的变形比远离荷载作用点的变形大得多，竖向荷载作用下，距荷载作用点较远的点有翘起的趋势。城墙在城楼荷载作用下的变形较小。

（4）从受力角度考虑，城墙的城门洞对台基强度有一定影响，这方面还需进一步研究。