利用沉降观测资料推算后期沉降量

对于大多数工程问题，次固结沉降与主固结沉降相比是不重要的。因此，地基的最终沉降量通常仅取瞬时沉降量与固结沉降量之和，即s=sd+sc。相应地，施工期T以后（t＞T）的沉降量为：

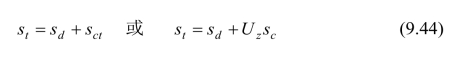
上式中的沉降量如按一维固结理论计算，其结果往往与实测成果不相符合，因为地基沉降多属于三维课题，而实际情况又很复杂，因此，利用沉降观测资料推算后期沉降（包括最终沉降量）有其重要的现实意义。下面介绍常用的两种经验方法：对数曲线法（三点法）和双曲线法（二点法）[4]。

1.对数曲线法

不同条件的固结度Uz的计算公式可用一个普遍表达式来概括：

式中，A和B是两个参数。如将上式与一维固结理论的公式进行比较，可见在理论上参数A是常数值8/π2，B则与时间因数Tv中的固结系数、排水距离有关。如果A和B作为实测的沉降与时间关系曲线中的参数，则其值是待定的。

将式（9.45）代入式（9.43），得：

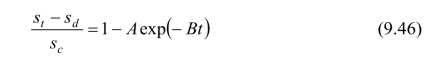
再将s=sd+sc代入上式，并以推算的最终沉降量s∞代替s，则得：

如果s∞和sd也是未知数，加上A和B，则式（9.47）包含4个未知数。从实测的早期s-t曲线（图9.23）选择荷载停止施加以后的三个时间t1、t2和t3，其中t3应尽可能与曲线末端对应，时间差（t2−t1）和（t3−t2）必须相等且尽量大些。将所选时间分别代入式（9.47），得：

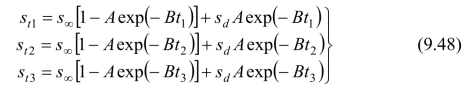
附加条件：

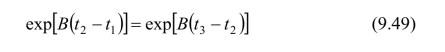
联解式（9.48）和式（9.49）可得：

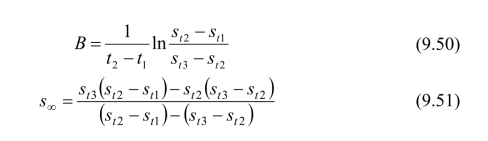(www.xing528.com)

将时间t1与st1、st2、st3实测值算得的B和s∞一起代入式（9.48），即可求得sd的计算表达式如下：

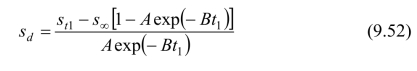
式中，参数A一般采用一维固结理论近似值8/π2，然后可按式（9.49）推算任一时刻的后期沉降量st。

以上各式中的时间t均应为修正后零点O′。工期荷载等速增长时，O′点在加荷期的中点，如图9.23所示。

2.双曲线法

建筑物的沉降观测资料表明其沉降与时间的关系曲线s-t接近于双曲线（施工期间除外），双曲线经验公式如下：

式中，s∞为推算最终沉降量，理论上所需时间t=∞；st1、st2为经历时间t1和t2出现的沉降量，时间应从施工期一半起算（假设为一级等速加荷）；at为曲线常数。

在式（9.53）中两组st1、t1和st2、t2为实测已知值，就可以求解出s∞和at的值如下：

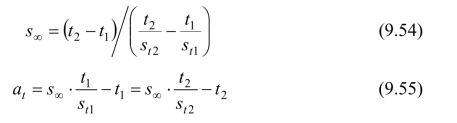
为了消除观测资料可能有的误差，包括仪器设备的系统误差、人为误差以及随机误差，一般将后段的观测点sti和ti都要加以利用，然后计算各ti/sti值，点在t～t/st直角坐标图上，其后段应为一直线（个别误差较大的点则剔除），如图9.24所示。从测定的直线段上任选两个代表性点（t1，st1）和（t2，st2）即可代入式（9.54）和式（9.55）确定最终沉降量s∞和at；此两值又代入式（9.53）确定后期任意时刻的沉降量。

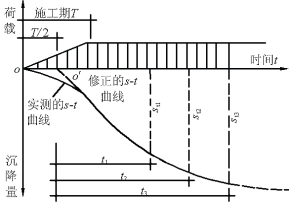
图9.23　沉降与时间关系实测曲线

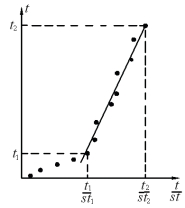
图9.24　双曲线法推算后期沉降量