广义剪应力双椭圆帽盖土力学模型

在帽盖模型中，广义屈服准则F和帽盖函数Φ一般都建立在两个独立假设的基础上，并且广义屈服准则F在三轴拉伸状态时形成尖角。

由于岩土介质的抗拉能力很差，因此需把头部截去而拟以光滑的曲面。有的用抛物线来逼近库伦剪切破坏线，或用抛物线和椭圆来表示屈服面，也有将尖角处用一个光滑曲面过渡并用于岩土数值计算，这样增加了一个附加的修正函数F′，形成了F′、F和Φ三段曲线的破坏屈服准则。

在以上工作和实验资料的基础上，俞茂宏和李跃明提出把广义屈服准则和帽盖函数加以合成的统一模型，即广义剪应力双椭圆帽盖模型，其形式为：

上式中，a、a′、b、b′和C为材料常数，σg、τg分别取单剪应力（τ13，σ13）、八面体应力（τ8，σ8）以及双剪应力（τtw，σtw）。由此可得到三个新的帽盖模型，分别称为广义单剪应力双椭圆帽盖模型、广义八面体剪应力双椭圆帽盖模型和广义双剪应力双椭圆帽盖模型。它们在σg和τg坐标中的图形由两个椭圆方程的曲线构成，如图8.11所示。

岩土类材料既有剪切破坏，又具有体积屈服。式（8.12a）中的Φ模拟了材料的脆性破坏且无尖角，而式（8.12b）中的Φ′则是满足体积塑性应变的帽盖。这里的双椭圆并不是破坏准则和帽盖模型两种函数（以往其他帽盖模型均为两种函数），而是同时满足上述两种破坏屈服条件的统一模型中的两个方程式，但也不是Meeh、Tokuoka等表述的一个封闭椭圆，在低围压情形时用一个封闭椭圆去反映岩土类材料的两种破坏屈服条件是不确切的。因此，双椭圆帽盖模型可较为灵活地适应各种不同的情况。

图8.11　双椭圆帽盖模型

双椭圆帽盖模型把破坏准则和帽盖模型统一为一个准则（两个方程，根据判别条件选用一个），方便了表述和使用，并且完全避免了线性破坏准则在拉伸区形成的尖角，可以与实验结果更为符合。式中的材料常数a、b和C可由常规的三轴试验来确定。a和a′、b和b′只相差一个常数，可根据材料性质调整。

下面讨论如图8.12所示的几种特殊应力状态，以确定常数a、b和C。

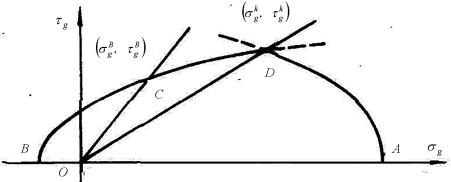
图8.12　双椭圆模型的参数

（1）A点：该点代表三轴均压（静水应力）产生屈服的应力状态，即σ1=σ2=σ3=p0，此时相应的广义正应力为：

此时式（8.12a）简化为：

（2）B点：该点代表三轴均拉极限应力状态，由于实际中三轴拉伸状态较难达到，可近似取单轴拉伸极限σt代替，即：

广义正应力为：

由式（8.12a）可得：

(www.xing528.com)

（3）设两椭圆的交点D的应力状态为，此时Φ=Φ′，即：

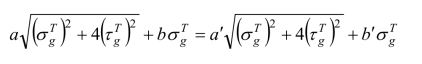
若令，则有：

（4）取一任意低围压侧限三轴压缩状态C，，其中系数γ<1。对于岩土类材料，这种试验是容易实现的。

当β>K时，由式（8.12a）可得：

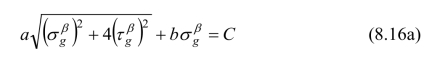
当β<K时，则由式（8.12b）可得：

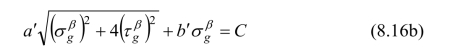
从以上所得各式联立解出a、b和C，即：

而a′=a −ξ，b′=b+η，其中称为材料的广义压拉特性比，η和ξ的选取应满足式（8.15），而K值则由试验资料确定。

为保证模型的双椭圆性，需满足C≠0，即材料的抗拉极限不能为零，故本章所建议的模型适用于具有抗拉强度的岩石、黏土及紧密砂类介质。基于岩土类介质的抗压极限大于抗拉极限的事实，即，可知α>1。从式（8.13）和（8.14）还可知（a-b）>（a′+b′）>0。

在以往的椭圆帽盖模型中，一般认为屈服轨迹椭圆的顶点与破坏迹线正好相交，无法反映土的剪胀性。后来黄文熙提出的模型克服了这一缺点。现在的模型中也无此限制，破坏准则Φ和屈服准则Φ′可在任意处相交，只需调整η和ξ的数值。适当选取η和ξ即可反映土的剪胀性，因而比前述各类椭圆模型有较大的适用范围，能拟合更多岩土材料的实验曲线。

若用于描述材料的硬化或软化特性，常数a′、b′和C是塑性内变量的函数。

当a≠b时，模型的标准椭圆方程如下[22-23]：

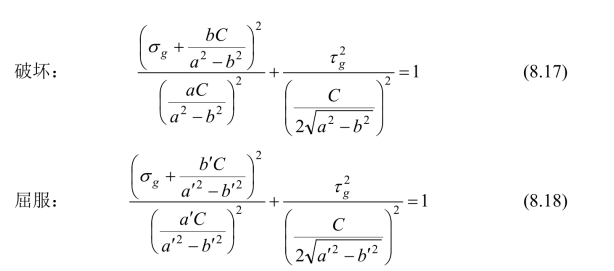
a=b时，模型为抛物线型。

近年来帽盖模型得到了较大发展和应用，美国已将其应用于原子防护工程、结构工程抗震设计、穿地动力学、核武器的攻击威力估算等研究中，并编入大型有限元计算程序，进行岩土工程和土与结构物相互作用的计算与研究[24]。此外，帽盖模型也应用于岩石和混凝土材料。例如，中国科学院北京力学研究所钱寿易和章根德[25]发表了文章《岩石的非线性弹性一塑性硬化帽盖模型》，华中科技大学卢应发等[26]发表了文章《广义帽盖模型和数值模拟》，长安大学、同济大学姜华等[27]发表了文章《混凝土弹塑性损伤帽盖模型参数确定研究》等。下面将介绍统一强度理论帽盖模型。