【摘要】:俞茂宏[21-23]1986年提出的双剪帽盖模型中,它的剪切破坏面由双剪强度理论的两个方程F和F′控制,体积屈服面采用椭圆方程Φ,其主应力空间的破坏面和屈服面如图8.9所示。图8.9双剪帽盖模型图8.10p-q平面的双剪帽盖模型双剪帽盖模型的破坏面和屈服面,由于采用了广义双剪强度理论,因而其范围均较前两类帽盖模型扩大了。因此,图8.10的双剪帽盖模型也可绘成如图8.7的剑桥帽盖模型的形式,两者一致。
俞茂宏[21-23]1986年提出的双剪帽盖模型中,它的剪切破坏面由双剪强度理论的两个方程F和F′控制,体积屈服面采用椭圆方程Φ,其主应力空间的破坏面和屈服面如图8.9所示。双剪帽盖模型在p-q平面的破坏线和屈服线如图8.10所示。
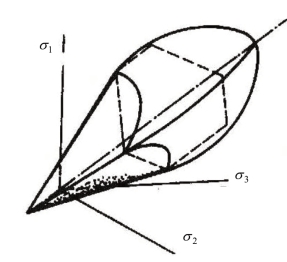
图8.9 双剪帽盖模型
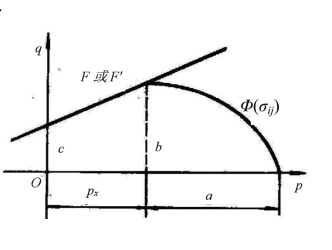
图8.10 p-q平面的双剪帽盖模型(https://www.xing528.com)
双剪帽盖模型的破坏面和屈服面,由于采用了广义双剪强度理论,因而其范围均较前两类帽盖模型扩大了。在具体应用时,与广义双剪强度理论相同,需注意不同的应力状态采用不同的破坏式F或F′,如下式所示:
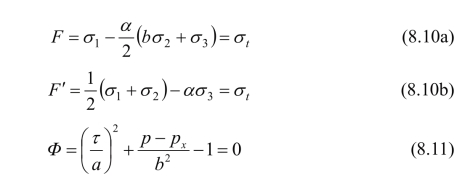
图8.10显示了相应的破坏线和屈服线,其中参数a、b、px与式(8.11)相对应,可以由试验资料来拟合确定。事实上,在p-q平面中所绘的曲线为θ=0°和θ=60°的子午极限线,而这一子午面的单剪强度理论和双剪强度理论是一致的。因此,图8.10的双剪帽盖模型也可绘成如图8.7的剑桥帽盖模型的形式,两者一致。式(8.10)的F式对应θ=0°时的极限线,式(8.10b)的F′式对应θ=60°时的极限线,两者的差别在0<θ<60°的其他子午线上,这时,双剪帽盖模型的极限线范围均大于单剪帽盖模型(剑桥模型)的极限线。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




