土力学新论：剑桥模型与帽盖模型对比

1958—1963年，英国剑桥大学Roscoe教授等人针对流经剑桥大学附近的Cam河的一种正常固结黏土和弱超固结黏土（湿黏土）的特性提出了一种新的弹塑性模型[6-11]，它包含一系列基本概念和假设，常被称为剑桥模型。

剑桥模型提出较早，发展也较完善，在一般土力学和岩土塑性力学书中已成为经典内容[12-18]。它的一个主要的结果是附加在莫尔-库仑强度理论极限面之上的状态边界面，称为Roscoe屈服面，如图8.6所示。

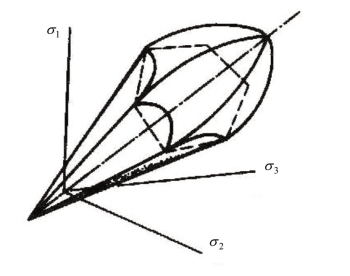
图8.6　剑桥模型（单剪帽盖模型）

最初提出的剑桥模型的屈服面为子弹头型，后来修改为椭球形。它在应力空间中是一个以原点为顶点、以静水应力轴为轴线的六边形锥体，附加一个半椭球形的“帽子”扣在六边形锥体的开口端。当单元体的应力处于屈服或破坏面以内时，材料处于弹性状态；应力点在屈服面上时，材料开始进入塑性状态；当应力点到达破坏面时，材料处于破坏状态。帽盖屈服面与破坏面的交线常称为临界状态迹线。剑桥模型为帽盖模型中的一种。

剑桥模型在p-q平面的屈服曲线方程可写为如下两种形式：

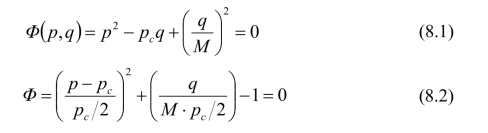
式中，pc为土固结压力（这里为硬化参数H，H=pc），M为破坏线直线斜率。(www.xing528.com)

剑桥模型在p-q平面的屈服曲线是一个以（0，pc/2）为中心，以pc/2为长半轴，以q=Mpc/2为短半轴的椭圆。由于拉压时的破坏线斜率M不同，故拉伸椭圆和压缩椭圆的短半轴长度也不相同，形成上下两个不同短半轴长度的半椭圆，如图8.7（a）所示。图8.7（b）为我国南京水利科学研究院魏汝龙于1964年提出的一种帽盖模型，它是对剑桥模型的修正，适用性比剑桥模型更普遍，但当γ=a=1/2时，两者相同。魏汝龙提出的帽盖屈服函数为.[19]：

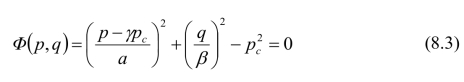
式（8.3）和式（8.2）均为椭圆方程。

剑桥模型之所以能得到广泛应用，是因为它能较好地适用于正常固结黏土和弱固结黏土，参数较少且易于测定。剑桥模型也有局限性，它的弹塑性矩阵中所有的元素均不为零，表示它能考虑土的剪胀和剪缩性，但实际上，由于剑桥模型的屈服轨迹斜率处处为负，塑性应变增量沿p方向的分量只能是正值即压缩，模型只能反映剪缩，不能反映剪胀，所以剑桥模型更适合应用于正常固结土或弱超固结土等一类具有压缩型体积屈服曲线的土体。

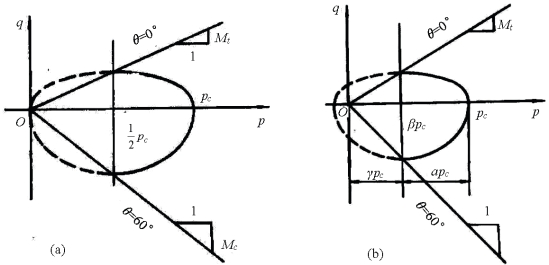
图8.7　单剪帽盖模型。（a）剑桥模型；（b）魏汝龙模型