新论：土力学强度孔水压方程

在饱和土的真三轴实验中，应力改变通常是由三个阶段引起的，假设由大主应力增量Δσ1引起的孔隙水压力为Δu1，Δσ2引起的为Δu2，Δσ3引起的为Δu3，则总的孔隙水压力为：

三维增量应力状态如图6.4所示。

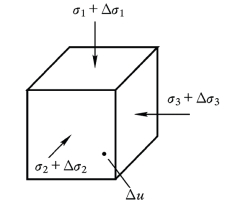
图6.4　三维增量应力状态

相应的有效应力为：

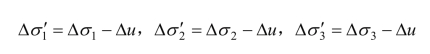
土单元体体积变化为：

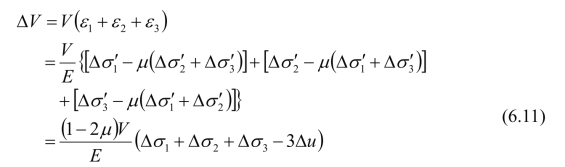
式中，V为土体体积，E为土骨架弹性模量，μ为土体泊松比。孔隙的压缩量为：

式中，Cw为流体的压缩性系数，n为孔隙率。

由式（6.11）和（6.12）相等可得：

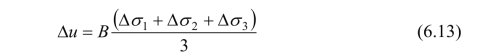
式中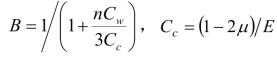，是土骨架的压缩系数。

孔隙水压力方程（6.13）可进一步变换形式为：

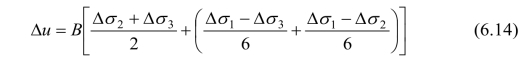
同样，我们考虑到土体并非完全线弹性体，故引入孔隙压力系数A和C，写成一般式为：(www.xing528.com)

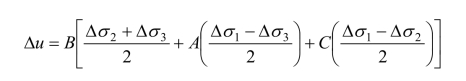
我们将俞茂宏统一强度理论推广到孔隙水压力方程，整理以上公式可以得到：

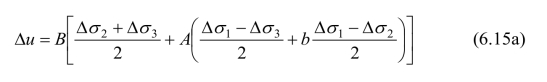
式中，b=C/A。

式（6.15a）可以写成统一强度理论的形式，即：

该公式的第二项正是剪应力增量Δτ13+bΔτ12所产生的孔隙水压，反映了中间主剪力对孔隙水压力的不同影响，用参数b来体现。当b=1时，为双剪孔隙水压力方程。当b=1且Δσ2=Δσ3，即常规三轴应力状态时，可自然转化为Skempton单剪孔隙水压力方程。因此，Skempton与双剪孔隙水压力方程均是统一强度孔隙水压力方程的特例。

值得注意的是，一些试验结果表明三轴伸长试验测得的A恰为三轴压缩试验A的两倍，因此有：

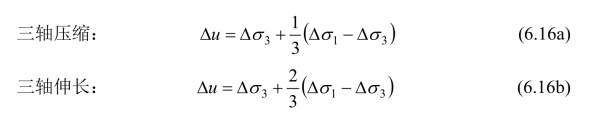
统一强度孔隙水压力方程式（6.15）若变换成与Skempton方程相似的形式（令A=C=1/6，即b=1），有：

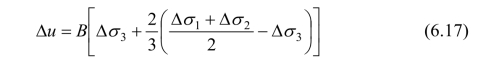
三轴伸长时Δσ1=Δσ2，式（6.17）可转化为（6.16b），所以考虑中间主应力增量变化后在理论上证明了这种两倍关系。

另外，Kars黏土在轴向伸长和侧向压缩试验中，其有效应力途径和应力-应变曲线虽然一致，但是绝对孔隙压力反应却不同。侧向压缩为加荷载状态产生正孔隙压力，如方程（6.14）所表达，而轴向伸长属卸荷载状态，形成负孔隙水压力。实际上可将式（6.14）转换成另一种形式，有：

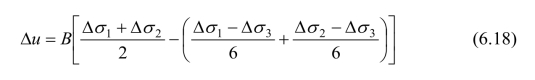
同理，式（6.18）写成一般形式为：

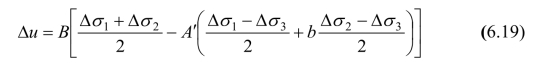
注意到系数A′前是负号，因此，这个方程恰好反映了这种三向伸长态的情况，而原Skempton单剪孔隙水压力方程是无法反映的，它可能只反映三轴压缩状态。统一强度孔隙水压力方程式（6.15a）和（6.15b）在中间主应力分量的大小不同时具有不同的表达式。