土力学新论：有效应力原理

有效应力原理被看作是现代土力学的核心。太沙基在1936年第一届国际土力学和基础工程大会上通俗易懂地阐述了这一原理。他认为，在土剖面上任何一点的应力（通过土体）可根据作用在这点上的总主应力（σ1，σ2，σ3）来计算。如果土中的孔隙是在应力u（孔隙应力）下被水充满，总主应力由两部分组成：一部分是u，以各个方向相等的强度作用于水和固体，这一部分称作孔隙水压力；另一部分为总主应力σ和孔隙水压力u之差，即σ′1=σ1−u、σ′2=σ2−u、σ′3=σ3−u，它只是在土的固相中发生作用，这一部分称作有效主应力（改变孔隙水压力实际上并不产生体积变化，孔隙水压力与在应力条件下土体产生破裂无关）。多孔材料（如砂、黏土和混凝土）对u所产生的反应似乎是不可压缩的，内摩擦等于零。改变应力所能测到的结果，诸如压缩、变形和剪切阻力的变化，仅仅是由有效应力σ′1、σ′2和σ′3的变化而引起的。因此，对饱和土体稳定性的调查研究需要具有总应力和孔隙水压力的知识。有效应力原理的实质是有效应力控制了土体的体积变化和强度。有效应力原理对于土体，特别是饱和土体来说基本上是正确的[1-20]。孔隙介质中的总应力等于有效应力加孔隙压力，它们之间的关系如图6.2所示。

图6.2　孔隙介质中的总应力σ=uw+σ′

太沙基的饱和土的有效应力公式为：

1955年，Bishop提出非饱和土中的有效应力公式为：

(www.xing528.com)

式中，ua为孔隙中的空气压力（简称孔隙气压力），uw为孔隙水压力，χ为一个与饱合度有关的参数（对于饱和土χ=1，干土χ=0）。

在有效应力方程的各项中，一般只有总应力σ可直接测得，孔隙压力可以通过粒间区之外的一点上测得。有效应力是一个推导出来的量，在工程中往往用粒间应力的概念来说明有效应力（在土力学文献中，有效应力和粒间应力这两个名词可以通用）。粒间力和孔隙压力（包括孔隙水压力uw和孔隙气压力ua）的示意图如图6.3所示。

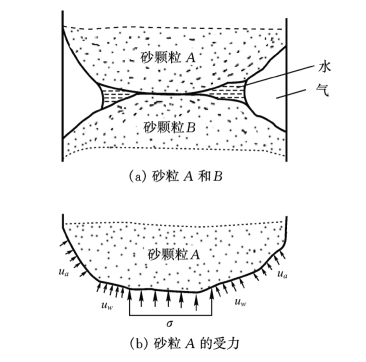
图6.3　粒间力和孔隙压力示意图

在有效应力原理中，孔隙压力是一个重要的概念。下面我们对土体中的孔隙水压力方程做进一步的研究。