土力学新论：b变化时的统一强度理论极限面

下面，我们将取b=0、b=1/4、b=1/2、b=3/4和b=1五种典型情况来进行研究。

(1)b=0

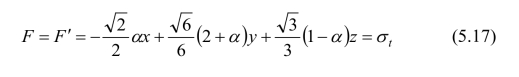
这就是莫尔-库仑强度理论的极限面，如图5.3中的虚线（最里边）所示。

(2)b=1/4

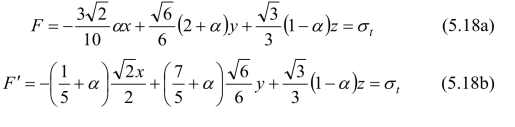
这是一个新的强度极限面，如图5.3（b）中的接近莫尔-库仑强度理论虚线（b=0）的极限迹线。

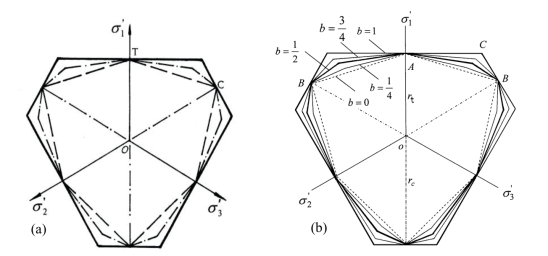
图5.3　统一强度理论的偏平面极限线。（a）统一强度理论的三个典型特例；（b）统一强度理论的五个典型特例

(3)b=1/2

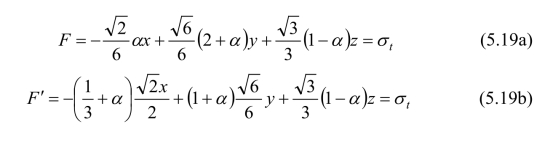(www.xing528.com)

此即为统一双剪强度理论的极限面。它居于莫尔-库仑单剪强度理论和双剪强度理论的中间，如图5.3中的中间极限迹线。它可以作为一个新的独立的强度理论得到应用。

(4)b=3/4

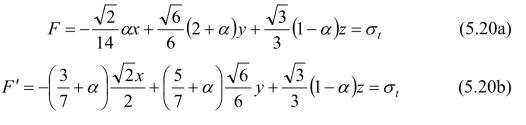
(5)b=1

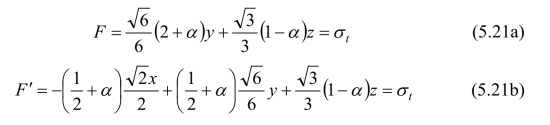
此即为双剪强度理论的数学表达式，它的极限面是图5.3中最外边的实线。

以上作图中都没有考虑z（即z=0的平面）。图5.3均为不同参数b值在某一相同z值时的极限线的相对大小和形状。如果将拉伸强度和拉压强度比与内摩擦角以及抗剪强度之间的关系公式代入式（5.21），则可得出：

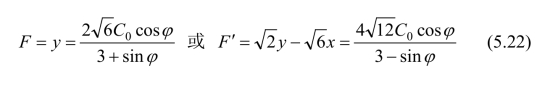
此即为双剪强度理论在偏平面的极限线方程。相应的方程特点和极限形状均相同。同理可以证明，b=0时的统一强度理论在偏平面的极限线即为莫尔-库仑强度理论的极限线；b=1/2时的统一强度理论极限线即为新破坏准则的极限线，所以它们均为统一强度理论的特例。图5.3为统一强度理论的三个典型特例和五个典型特例时的极限迹线。

统一强度理论还可以退化得出更多的计算准则。图5.4给出了统一强度理论系数b和拉压强度比α改变时，统一强度理论的极限迹线的一系列变化规律。