土力学新论：统一强度理论的力学模型

在土力学和一般力学中，常常采用主应力状态（σ1，σ2，σ3）来进行研究。20世纪80年代，俞茂宏将主应力状态转换为主剪应力状态（τ13，τ12，τ23）。由于三个主剪应力中恒有等式（τ13=τ12+τ23），因此，三个主剪应力中只有两个独立量。根据这一基本概念，俞茂宏将它们转换为双剪应力状态（τ13，τ12；σ13，σ12）或（τ13，τ23；σ13，σ23），并提出和建立了一种新的正交八面体的双剪单元体[11-16]。

两组剪应力共八个作用面形成了一种新的八面应力单元体，从而得出两个相应的双剪单元体力学模型，如图5.1所示。双剪单元体是一种扁平的正交八面体，在它们的两组相互垂直的四个截面上作用着最大主剪应力τ13和次大主剪应力τ12（图5.1（a））或τ23（图5.1（b））。这是由于三个主剪应力τ13、τ12和τ23中，虽然只有两个独立量，但中间主剪应力可能为τ12，也可能为τ23，因此，必须根据应力状态的特点来在τ12和τ23中确定较大者。

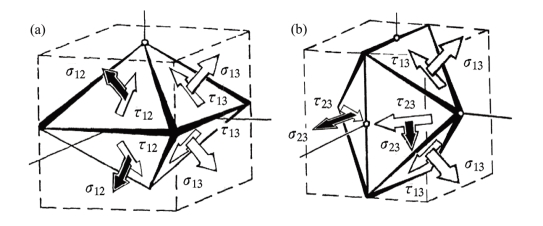
图5.1　双剪单元体力学模型。（a）（τ13，τ12；σ13，σ12）；（b）（τ13，τ23；σ13，σ23）(www.xing528.com)

双剪单元体虽然是一个新的模型，但并不是特别的概念，它只是从主应力单元体派生出来的新的力学模型。双剪单元体也可派生出新的单元体，如将正交八面体一截为二，可得出一种新的四棱锥体单元体，在这两个四棱锥单元体上可以看到双剪应力与主应力σ1或σ3的平衡关系。正交八面体和它们的1/2单元体都是双剪应力单元体，它们将作为我们建立统一强度理论的物理或力学模型。

下面从这个统一的物理模型出发，考虑所有剪应力分量和它们面上的正应力分量对材料破坏的不同影响，提出一个能够适用于各种岩土类材料的新的统一强度理论和统一形式的数学表达式，莫尔-库仑强度理论和双剪强度理论均为其特例。它还包含了可以比Drucker-Prager准则更合理的新的计算准则，以及可以描述非凸极限面试验结果的新的非凸强度理论。